Ábrahám Gábor: Az $f^{-1}(x)=f(x)$ típusú egyenletekről, avagy az írástudók felelőssége és egyéb érdekességek

Az alábbi cikk a 2010. évi Rátz László Vándorgyűlésen elhangzott előadásom alapján készült.

Immár 18 éve tanítok a szegedi Radnóti Miklós Kísérleti Gimnázium matematika tagozatán. A tagozatunk fő feladata a tehetséggondozás, a matematika versenyekre történő felkészítés. Ennek nagyon fontos részét képezi, hogy olyan módszereket, ötleteket, fogásokat adjunk át a diákoknak, melyeket hatékonyan tudnak használni a munkájuk során. Ezeket mi is hosszú évek alatt sajátítottuk el sok tanulással, feladatmegoldással. A mi felelősségünk többek között abban áll, hogy az általunk közreadott megoldások precízek legyenek, a felhasznált tételeket pontosan fogalmazzuk meg, hogy azok alkalmazása nehogy hibás, vagy hiányos megoldásra vezessen. Ennek kapcsán szeretnék szólni az $f^{-1}(x)=f(x)$ típusú egyenletekről (ahol $f^{-1}(x)$ az $f(x)$ függvény inverze), melyekkel jó néhányszor találkozhattunk már matematika versenyeken.

Az első két feladat is versenyfeladat volt. Az itt közölt megoldásuk szó szerint az úgynevezett hivatalos megoldás. Ezekben kiemeltem azokat a részeket, melyekkel a cikk során részletesen foglalkozom.

1. feladat: Oldjuk meg a valós számok halmazán a

$6\frac{x^2+1}{x^2+11}=\sqrt{\frac{11x-6}{6-x}}$

(KöMaL F. 2830., NMMV 2003., KöMaL B. 4027. Az F. 2830. megoldása nem jelent meg a Lapban, ezért a feladatot más feladatokhoz hasonlóan 2003-ban B. 4027. számmal újra kitűztük. Ennek megoldása már megjelent a Lapban, lásd KöMaL, 2008/4., 220. oldal.)

Megoldás (NMMV 2003. hivatalos megoldása): Nézzük a jobb oldali függvényt, ennek egyenlete: $y=\sqrt{\frac{11x-6}{6-x}}$. Ezt $x$-re rendezve $x=6\frac{y^2+1}{y^2+11}$ adódik. Látható tehát, ha az egyik oldalt az $x$ függvényének tekintjük, akkor a másik oldal az előbbi inverz függvénye. A két függvény képe egymás tükörképe az $y=x$ egyenesre nézve, ezért metszéspontjaik az $y=x$ egyenesen vannak. Így elegendő az $x=\frac{6(x^2+1)}{x^2+11}$ egyenletet megoldani. A rendezés utáni $x^3-6x^2+11x-6=0$ egyenlet bal oldalának szorzat alakja $(x-1) (x-2) (x-3)=0$. Ez alapján az egyenlet megoldásai az 1, 2, 3 számok, melyek igazzá is teszik az eredeti egyenlőséget.

$*$

Ezzel a hivatalos megoldás végére értünk.

A lelkiismeretünk megnyugtatása végett ábrázoljuk az

$f\colon \mathbb{R}\to \mathbb{R};\quad f(x)=6\frac{x^2+1}{x^2+11}$

és a

$g\colon \left[\frac{6}{11};6\right[ \to \mathbb{R};\quad g(x)=\sqrt{\frac{11x-6}{6-x}}$

függvényt (1. ábra).

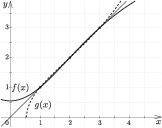
1. ábra

Az ábra alapján az alábbi megállapításokat tehetjük:

- A két függvény grafikonja az $y=x$ egyenesen metszi egymást, tehát a megoldásnak ez a része látszólag rendben van.

- A figyelmes szemlélő számára látható az $f$ függvény grafikonján, hogy a függvény nem kölcsönösen egyértelmű. Erre annak alapján is felfigyelhetünk, hogy az $f$ függvény páros, hisz minden $x\in D_f$ esetén $-x\in D_f$ is teljesül, és

$f(-x)=6\frac{{(-x)}^2+1}{{(-x)}^2+11}=6\frac{x^2+1}{x^2+11}=f(x).$

Tehát kézenfekvő az alábbi kérdés: Korrekt volt az inverz kapcsolat említése?

Mielőtt a kérdéssel behatóbban foglalkoznánk, nézzünk meg egy másik versenyfeladatot, melyet 2003-ban tűztek ki a Nemzetközi Magyar Matematika Versenyen.

2. feladat: Oldjuk meg a valós számok halmazán a $\log_3 (2^x+5)=\log_2 (3^x-5)$ egyenletet.

(NMMV 2003.)

(A hivatalos megoldás az alábbi volt.)

Megoldás: Vizsgáljuk az alábbi két függvényt:

$\begin{array}{rlrl} f & \colon \mathbb{R}\to \left]\log_3 5;\infty\right];& f(x) & =\log_3 (2^x+5), \\ g & \colon \left]\log_3 5;\infty\right] \to \mathbb{R}; & g(x) & =\log_2 (3^x-5). \end{array} ~~~~~(1)$

Mivel a két függvény egymás inverze, a grafikonjuk az $y=x$ egyenesre nézve szimmetrikus, így grafikonjaik csak ezen az egyenesen metszhetik egymást.

Ezért az egyenletnek csak olyan $x$ szám lehet a megoldása, amelyre

$\log_3 (2^x+5)=x=\log_2 (3^x-5),$

vagyis $2^x+5=3^x$. Ebből az $5=3^x-2^x$ egyenlethez jutunk, aminek csak a pozitív számok halmazán lehet megoldása, hiszen a nempozitív számok halmazán a jobb oldali kifejezés első tagja nem nagyobb a második tagjánál.

Az $x=$2 megoldás, több megoldás pedig azért nincs, mert a $3^x-2^x$ függvény a pozitív számok halmazán szigorúan monoton növekvő.

$*$

Érdemes megjegyezni, hogy utolsó megállapítás mindenképpen bizonyítást igényel. Az $f\colon \mathbb{R}^+\to \mathbb{R}$; $x\mapsto 3^x$ és a $g\colon \mathbb{R}^+\to \mathbb{R}$; $x\mapsto 2^x$ függvény is szigorúan monoton növekvő, és két szigorúan monoton növekvő függvény különbsége nem feltétlenül szigorúan monoton növekvő. Ebben az esetben viszont igen, hiszen

$3^x-2^x= 2^x\left[\left(\frac{3}{2}\right)^{x}-1\right],$

valamint minden $x\in \mathbb{R}^+$ esetén $2^x>0$, $\left(\frac{3}{2}\right)^{x}-1>0$ és mindkét tényező szigorúan monoton növekvő.

Ábrázoljuk az (1) függvényeket (2. ábra). A grafikon újfent megerősíteni látszik azt a gondolatot, mely szerint, ha egy invertálható függvény és inverzének a grafikonja metszi egymást, akkor a metszéspontnak az $y=x$ egyenesen kell lennie.

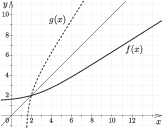
2. ábra

A továbbiakban alkalmazzuk a hivatalos megoldásokban látott gondolatmeneteket, módszereket.

3. feladat: Határozzuk meg a következő egyenlet valós megoldásait.

$\sqrt{2x+6} =\frac{x^2-6}{2}\,.$

(Alkalmazzuk szó szerint az 1. feladatra közölt hivatalos megoldást.)

Megoldás: Nézzük a bal oldali függvényt, ennek egyenlete: $y=\sqrt{2x+6}$. Ezt $x$-re rendezve $x=\frac{y^2-6}{2}$ adódik. Látható tehát, hogy ha az egyik oldalt az $x$ függvényének tekintjük, akkor a másik oldal az előbbi inverz függvénye. A két függvény képe egymás tükörképe az $y=x$ egyenesre nézve, ezért metszéspontjaik az $y=x$ egyenesen vannak. Így elegendő az $x=\frac{x^2-6}{2}$ egyenletet megoldani. Ennek megoldásai: $x_1 =1+\sqrt 7$; $x_2 =1-\sqrt 7$.

Ellenőrzéssel meggyőződhetünk arról, hogy a második szám nem megoldása az egyenletnek, mert a bal oldal pozitív, a jobb oldal negatív értékű. Az első viszont kielégíti az egyenletet.

$*$

Nyugtassuk meg a lelkiismeretünket, és ábrázoljuk az $f\colon \left[-3;\infty\right[ \to \mathbb{R}$; $f(x)=\sqrt{2x+6}$, valamint a $g\colon \mathbb{R}\to \mathbb{R}$; $g(x)=\frac{x^2-6}{2}$ függvényt (3. ábra).

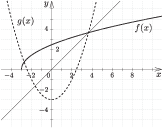
3. ábra

A grafikonok két pontban metszik egymást. Eszerint az egyenletnek két valós megoldása van, szemben azzal, amit az előző megoldásban kaptunk.

Hol a hiba a korábbi gondolatmenetben? Miért veszítettünk megoldást az előző feladatban?

Az egyik hibát ott követtük el, hogy az inverz kapcsolat vizsgálata esetén csak formális algebrai átalakításokat végeztünk, és nem foglalkoztunk az e mögött rejlő matematikai tartalommal.

Adjuk meg a feladathoz kapcsolódó két kölcsönösen egyértelmű függvényt, melyek egymás inverzei. Ezek az

$f\colon \left[-3;\infty\right[ \to \mathbb{R}_0^+; \ \ x\mapsto \sqrt{2x+6} \quad\mbox{ és a }\quad g\colon \mathbb{R}_0^+ \to \left[-3;\infty\right[; \ \ x\mapsto \frac{x^2-6}{2}$

függvények. Ha az egyenletet a $D_f \cap D_g =\mathbb{R}_0^+$ halmazon oldjuk meg, akkor az egyetlen megoldás tényleg az $x_1 =1+\sqrt 7$ szám. De a

$\sqrt{2x+6} =\frac{x^2-6}{2}$

egyenlet értelmezési tartománya nem az $\mathbb{R}_0^+$, hanem a $\bigl[-3;-\sqrt 6\,\bigr]\cup \bigl[\sqrt 6;\infty\bigr[$ halmaz. Ezen a halmazon viszont két megoldása van. Adjunk a feladatra korrekt megoldást.

I. megoldás: A $\bigl[-3;-\sqrt 6\,\bigr]\cup \bigl[\sqrt 6;\infty\bigr[$ halmazon az egyenlet mindkét oldala nemnegatív értékű, így négyzetre emeléssel az eredetivel ekvivalens egyenlethez jutunk. Végezzük el a négyzetre emelést és redukáljunk nullára:

$x^4-12x^2-8x+12=0.$

Mivel az $f$ és $g$ függvény grafikonja az $y=x$ egyenesen metszi egymást, az ${x=\frac{x^2-6}{2}}$ egyenlet megoldásai gyökei lehetnek az előző negyedfokú egyenletnek is. Így azt várjuk, hogy $x^2-2x-6$ osztója az $(x^4-12x^2-8x+12)$-nek. A polinomosztást elvégezve kapjuk, hogy

$x^4-12x^2-8x-12= (x^2-2x-6) (x^2+2x-2).$

Így az eredeti egyenlet megoldásai, az $x^2-2x-6=0$ és az $x^2+2x-2=0$ másodfokú egyenletek megoldásai közül kerülnek ki, melyek az $1+\sqrt 7$; $1-\sqrt 7$; $-1+\sqrt 3$; $-1-\sqrt 3$ számok.

Ezek közül az értelmezési tartománynak csak az $1+\sqrt 7$; $-1-\sqrt 3$ számok az elemei.

2. megoldás: A $\bigl[-3;-\sqrt 6\,\bigr]\cup \bigl[\sqrt 6;\infty\bigr[$ halmazon keressük az $y=\sqrt{2x+6}$ és az $y=\frac{x^2-6}{2}$ egyenletű görbék metszéspontjainak első koordinátáját. Emeljük négyzetre az első egyenletet, majd adjuk hozzá a második kétszeresét. Ekkor az $y^2+2y=x^2+2x$ kétismeretlenes egyenlethez jutunk, melyet könnyen szorzattá alakíthatunk: $(y-x)(y+x+2)=0$. Ebből kapjuk, hogy $y=x$ vagy $y=-x-2$. Ezt visszahelyettesítve a második egyenletbe az $x=\frac{x^2-6}{2}$ és a $-x-2=\frac{x^2-6}{2}$ egyenletekhez jutunk. Innen pedig megkaphatjuk a megoldásokat.

$*$

Könnyen gyárthatunk az előzőhöz hasonló egyenleteket. Az alábbiakban oldjunk meg még egy ilyen típusút.

4. feladat: Oldjuk meg a valós számok halmazán a $\sqrt[3]{2-x}=2-x^3$ egyenletet.

Megoldás: Az $f\colon \mathbb{R}\to \mathbb{R}$; $f(x)=2-x^3$ függvény nyilván kölcsönösen egyértelmű, így létezik inverze. Könnyen látható, hogy ez a $g\colon \mathbb{R}\to \mathbb{R}$; $g(x)=\sqrt[3]{2-x}$ függvény, hisz $D_g =R_f$, $R_g =D_f$, valamint

$f\big(g(x)\big)= 2-\big(\sqrt[3]{2-x}\,\big)^3=2-(2-x)=x.$

Az eddig jól működő gondolatmenet alapján az $f$ és $g$ függvény grafikonja csak az $y=x$ egyenesen metszheti egymást, így a $2-x^3=x$ egyenlethez jutunk. Ezt átrendezve és szorzattá alakítva kapjuk az $(x-1)(x^2+x+2)=0$ egyenletet, melynek csak $x=1$ a megoldása.

$*$

Ábrázoljuk az $f$ és $g$ függvényeket (4. ábra).

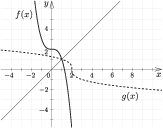
4. ábra

Úgy tűnik, a grafikon továbbra is igazolja a megoldásban alkalmazott gondolatmenetet. Az előző feladatban szereplő $f$ függvényből kiindulva foglalkozzunk az $f_c :\mathbb{R}\to \mathbb{R}$; $x\mapsto 2-{(x-c)}^3$ függvénnyel, ahol $c$ nemnegatív valós paraméter. Mivel $f_c$ bármely $c$ esetén kölcsönösen egyértelmű, azért létezik inverze.

Adjuk meg ezt az inverz függvényt. Fejezzük ki az $y=2-{(x-c)}^3$ egyenletből az $x$-et. Ekkor az $x=c+\sqrt[3]{2-y}$ egyenlethez jutunk. Ha felcseréljük $x$-et és $y$-t, akkor megkapjuk az $f_c$ függvény inverzének hozzárendelési szabályát. Tehát $f_c$ inverze az $f_c^{-1} :\mathbb{R}\to \mathbb{R}$; $x\mapsto c+\sqrt[3]{2-x}$ függvény.

Ábrázoljuk néhány $c$ érték esetén az $f_c$ függvényt és inverzét. A $c=0$ esetet már láttuk, legyen $c=0{,}5$, $c=0{,}8$, $c=1$ (5. ábra).

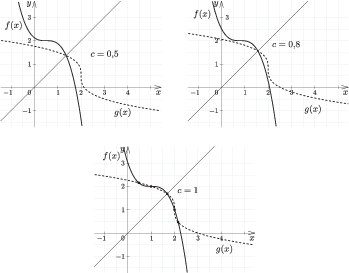
5. ábra

A grafikon alapján kijelenthetjük, hogy az ${(1-x)}^3+2=1+\sqrt[3]{2-x}$ egyenletnek öt valós megoldása van, melyek közül négyhez tartozó metszéspont nincs rajta az $y=x$ egyenesen.

Tehát hibás az az állítás, hogy ha egy invertálható függvény és inverzének a képe metszi egymást, akkor a metszéspont az $y=x$ egyenesen van!

Oldjuk meg az előző egyenletet.

Megoldás: Legyen $y=1-x$. Ekkor az $y^3+1=\sqrt[3]{1+y}$ egyenletet kapjuk, melyet köbre emelve és rendezve az $y^9+3y^6+3y^3-y=0$ egyenlethez jutunk. Ennek az $y=0$, így az eredetinek az $x=1$ megoldása, ahogy azt a grafikonról is leolvashattuk. Az $y$ kiemelésével kapott $y^8+3y^5+3y^2-1$ nyolcadfokú polinomnak az $y=-1$ gyöke, hisz az együtthatók váltakozó előjelű összege 0 (a hiányzó tagok együtthatója 0, és ezt figyelembe kell venni). Ebből kapjuk az eredeti egyenlet grafikonról is leolvasható másik egész gyökét, az $x=2$-t.

Az előzőek alapján $y+1$ osztója az $(y^8+3y^5+3y^2-1)$-nek, a hányados\-polinomot a Horner-féle elrendezés ([3], 284. oldal) segítségével könnyedén meg\-határozhatjuk. Így kapjuk, hogy

$y^8+3y^5+3y^2-1=(y+1) \big(y^7-y^6+y^5+2y^4-2y^3+2y^2+y-1\big).$

Mivel a két grafikon metszi egymást az $y=x$ egyenesen, az $x={(1-x)}^3+2$ egyenlet valós gyöke, megoldása az eredeti egyenletnek is. Áttérve $y$-ra azt kapjuk, hogy az $y^3+y+1=0$ egyenlet valós megoldása gyöke az

$y^7-y^6+y^5+2y^4-2y^3+2y^2+y-1$

hetedfokú polinomnak is. Ennek alapján azt várjuk, hogy

$y^3+y+1 \quad\mbox{osztója az}\quad \big(y^7-y^6+y^5+2y^4-2y^3+2y^2+y-1\big)\mbox{-nek,}$

ami teljesül is, amint arról polinomosztással meggyőződhetünk, $y^4-y^3+2y-1$ a hányados polinom. Tehát a feladatot visszavezettük az $y^3+y+1=0$ és az $y^4-y^3+2y-1=0$ egyenletek megoldására. Ebből meghatározhatjuk a még hiányzó három valós gyököt. (Lásd [3], 321-332. oldal.)

$*$

A továbbiakban foglalkozzunk a középiskolából jól ismert klasszikus inverz kapcsolattal.

5. feladat: Mely egytől különböző pozitív valós $a$ esetén van legalább egy valós megoldása az $a^x=\log_a x$ egyenletnek?

Megoldás: Látható, hogy a feladat ekvivalens azzal a kérdéssel, hogy mely egytől különböző pozitív valós $a$ esetén van legalább egy közös pontja az $f\colon \mathbb{R}\to \mathbb{R}^+$; $x\mapsto a^x$ és a $g\colon \mathbb{R}^+\to \mathbb{R}$; $x\mapsto \log_a x$ függvény grafikonjának.

Az eddigiek alapján csak annyit állíthatunk, hogy ha van közös pontjuk, akkor azok között biztosan található olyan, amelyik eleme az $y=x$ egyenesnek, hisz az $f$ és $g$ függvény folytonos az értelmezési tartományán.

Az eddigi ismereteink alapján nyilvánvaló, hogy ha $0< a <1$, akkor a két grafikon metszi egymást. Legyen ezután $a>1$.

Ábrázoljuk $a=10$, illetve $a=1{,}3$ esetén a függvényeket. Az $y=x$ egyenes elválasztja a két grafikont $a=10$ esetén, illetve belemetsz a grafikonokba $a=1{,}3$ esetén (6. ábra).

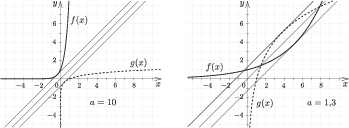
6. ábra

Mivel a $g$ függvény szigorúan konkáv, a következőt állíthatjuk. Az $f$ és $g$ függvény grafikonjának $a>1$ esetén akkor és csak akkor van közös pontja, ha a $g$ grafikonjának az $y=x$ egyenessel párhuzamos érintője az $y$ tengelyt a nemnegatív tartományban metszi.

Határozzuk meg az érintő egyenletét. Mivel az érintő meredeksége 1 és

$g'(x)=\frac{1}{x\cdot \ln a}\,,$

az érintési pont $x$ koordinátája $x=\frac{1}{\ln a}$. Tehát az érintési pont az $E\left(\frac{1}{\ln a};\log_a\frac{1}{\ln a}\right)$ pont. Az $y$ koordinátából látszik, hogy ez a pont csak $a>1$ esetén létezik. Az érintő egyenlete:

$y=x-\frac{1}{\ln a}+\log_a \frac{1}{\ln a}.$

Az $f$ és $g$ grafikonjának akkor és csak akkor van közös pontja, ha

$\frac{1}{\ln a}\le \log_a \frac{1}{\ln a}=-\log_a \ln a=-\frac{\ln\, (\ln a)}{\ln a}.$

Ezt végigszorozva a negatív $-\ln a$-val az $1\ge \ln\, (\ln a)$ egyenlőtlenséghez jutunk. Használjuk fel, hogy $e>1$.

$$\begin{gather*} 1\ge \ln\, (\ln a) \\ \Updownarrow \\ \frac{1}{e}\ge \ln a \\ \Updownarrow \\ e^{\frac{1}{e}}\ge a \end{gather*}$$

Tehát a vizsgált paraméteres egyenletnek akkor és csak akkor van valós megoldása, ha $0<a<1$ vagy $1<a\le e^{\frac{1}{e}}$ (7. ábra).

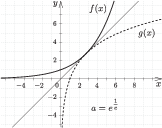
7. ábra

$*$

Az előző feladat után kézenfekvő az alábbi kérdés.

6. feladat: Az $5$. feladatban szereplő egyenletnek az $a$ paraméter mely értékeinél van $1$, illetve $2$ valós megoldása? Van-e olyan $a$ érték, amely esetén az egyenletnek kettőnél több valós megoldása van?

Megoldás: Az előző feladatban láttuk, hogy ha $1<a<e^{\frac{1}{e}}$, akkor az egyenletnek két megoldása van, ha $a=e^{\frac{1}{e}}$, akkor egy. Vizsgáljuk meg a $0<a<1$ esetet; készítsünk néhány ábrát (8. ábra).

8. ábra

Vizsgáljuk meg, hogy milyen feltételek mellett van három metszéspontja a két görbének. Húzzuk be mindkét görbe érintőjét az $y=x$ egyenesre eső $P(x_0;x_0)$ pontba (9. ábra).

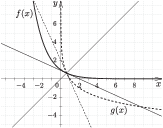
9. ábra

Lehet-e olyan eset, hogy a két görbe érintője megegyezik?

Mivel a két görbe egymás tükörképe az $y=x$ egyenesre nézve, a $P$ pontba húzott érintőik is egymás tükörképei erre az egyenesre nézve. Tehát a két érintő csak úgy eshet egybe, ha merőleges az $y=x$ egyenesre, így iránytangense $-1$, azaz irányszöge $-45^\circ$.

Használjuk fel, hogy $a^{x_0}=x_0$, és az exponenciális függvény deriváltja az $x_0$ pontban $-1$, tehát $a^{x_0}\cdot \ln a=-1$. Így $a=\left(\frac{1}{e}\right)^{e}$ (10. ábra).

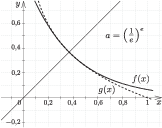
10. ábra

Ha $\left(\frac{1}{e}\right)^{e} <a <1$, akkor az exponenciális függvény $P(x_0;x_0)$ pontjába húzott érintőjének a meredeksége negatív, de nagyobb $-1$-nél. Így a $P$ pontba húzott érintő irányszögének abszolút értéke kisebb $45^\circ$-nál, a logaritmus függvényé nagyobb. Ezért az $x_0$-nak van olyan jobb oldali környezete, amelybe eső $x$-ek esetén a logaritmus függvény grafikonja az exponenciális függvényhez húzott érintő alatt halad, míg az exponenciális függvény grafikonja az érintő fölött. Az $a <1$ alapú logaritmus függvény $x_0 < x$ abszcisszájú pontjaiba húzott érintőinek a meredeksége kisebb, mint az inverze ugyanilyen abszcisszájú pontjába húzott érintőjének meredeksége. Így a két grafikon csak a $P$ pontban metszi egymást.

Ha $0 < a<\left(\frac{1}{e}\right)^{e}$, akkor az exponenciális függvény $P$-beli érintőjének az irányszöge a nagyobb abszolút értékű. Így a $P$ abszcisszájának van olyan bal oldali környezete, ahol a logaritmus függvény grafikonja az exponenciális függvény grafikonja alatt halad (lásd a 11. ábrát). Valahol viszont bele kell metszenie, mert az exponenciális függvény grafikonja metszi az $y$ tengelyt, a logaritmus függvényé nem. Több metszéspont pedig nem jön létre, mert a tengelyek elválasztják a grafikonokat.

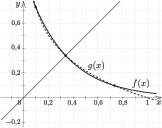
11. ábra

Összegzés: Az $a^x=\log_a x$ ($0< a$, $a \ne 1$) egyenletnek:

– nincs valós megoldása, ha $e^{\frac{1}{e}} < a$;

– egy valós megoldása van, ha $a=e^{\frac{1}{e}}$, vagy $\left(\frac{1}{e}\right)^e\le a <1$;

– két valós megoldása van, ha $1< a < e^{\frac{1}{e}}$;

– három valós megoldása van, ha $0< a<\left(\frac{1}{e}\right)^e$.

$*$

Térjünk vissza az 1., majd a 2. feladatra. Először adjunk az 1.-re egy olyan megoldást, amely elkerüli a két oldal közötti inverz kapcsolat felhasználását.

1. feladat: Oldjuk meg a valós számok halmazán a

$6\frac{x^2+1}{x^2+11}=\sqrt{\frac{11x-6}{6-x}}$

egyenletet.

Megoldás: (Ezzel a megoldással lényegében azonos a B. 4027.-es feladatra adott KöMaL internetes megoldás, amely a http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=B4027&l=hu oldalon olvasható.)

Az egyenlet értelmezési tartománya a $\left[\frac{6}{11};6\right[$ intervallum. Emeljük négyzetre az egyenletet, majd redukáljunk nullára. Ekkor a

$47x^5-222x^4+314x^3-564x^2+1367x-942=0$

egyenlethez jutunk. Mivel az együtthatók összege 0, azért $x=1$ gyöke az egyenletnek, tehát

$x-1\quad\mbox{osztója a}\quad \big(47x^5-222x^4+314x^3-564x^2+1367x-942\big)\mbox{-nek.}$

Horner-elrendezéssel vagy polinomosztással meghatározhatjuk a hányadost, amely a

$47x^4-175x^3+139x^2-425x+942$

polinom. Ha ennek van egész gyöke, akkor az csak a konstans tag osztói közül kerülhet ki. Könnyen meggyőződhetünk arról, hogy $x= 2$ gyök. Így

$x-2 \quad\mbox{osztója a}\quad \big(47x^4-175x^3+139x^2-425x+942\big)\mbox{-nek.}$

A hányados megint meghatározható Horner-elrendezéssel vagy polinomosztással, amely a

$47x^3-81x^2-23x-471$

polinom. Ennek $x=3$ gyöke, így a polinom osztható $(x-3)$-mal. A hányados a $47x^2+60x+157$, melynek nincs valós gyöke, mivel a diszkriminánsa negatív. Tehát az egyenlet megoldásai az 1, 2, 3 számok.

$*$

A 2. feladat kapcsán, az ábra alapján már meggyőződtünk arról, hogy az $f(x)=\log_3 (2^x+5)$ és a $g(x)=\log_2 (3^x-5)$ függvények grafikonja csak az $y=x$ egyenesen metszi egymást. Ezt most bizonyítsuk is be!

Azt már bebizonyítottuk, hogy az $f(x)=\log_3 (2^x+5)$ és a $g(x)=\log_2 (3^x-5)$ függvények grafikonjának az $y=x$ egyenesen csak az $x=2$ helyen van metszéspontja, mert a $\log_3 (2^x+5)=x= \log_2 (3^x-5)$ egyenletnek csak az $x=2$ a megoldása.

Megmutatjuk, hogy az $f$ függvény az értelmezési tartományán szigorúan konvex, a $g$ pedig szigorúan konkáv.

Az $f$ első deriváltja

$f'(x)=\big(\log_3 (2^x+5)\big)' =\frac{\ln 2\cdot 2^x}{\ln 3\cdot (2^x+5)}\,,$

így a második derivált

$f''(x)=\left(\frac{\ln 2\cdot 2^x}{\ln 3\cdot (2^x+5)}\right)' =\frac{\ln^22\cdot 2^x}{\ln 3} \,\frac{5}{{(2^x+5)}^2}\,,$

ami bármely valós $x$ esetén pozitív, tehát $f$szigorúan konvex függvény. A $g$ függvény első deriváltja

$g'(x)= \big(\log_2 (3^x-5)\big)' =\frac{\ln 3\cdot 3^x}{\ln 2\cdot (3^x-5)}\,.$

A második deriváltja

$g''(x)=\left(\frac{\ln 3\cdot 3^x}{\ln 2\cdot (3^x-5)}\right)' =\frac{\ln^23\cdot 3^x}{\ln 2}\, \frac{-5}{{(3^x-5)}^2}\,,$

ami a $g$ értelmezési tartományának bármely $x$ értékére negatív, így a $g$ az értelmezési tartományán szigorúan konkáv.

Az eddigiekből következik, hogy a 2-nél kisebb helyeken az $f$ függvény grafikonjának minden pontja az $y=x$ egyenes felett, a $g$ függvényé pedig az alatt helyezkedik el, tehát itt nem metszhetik egymást, míg a 2-nél nagyobb helyeken fordított a helyzet, így ott sem metszhetik egymást. Ezzel igazoltuk, hogy a két grafikonnak csak az $x=2$ helyen van közös pontja.

$*$

Konklúzió:

- Nagyon fontos, hogy két függvény közötti inverz kapcsolat bizonyítása ne csak formális algebrai átalakítás legyen, hanem ennél mélyebb megfontolás.

- Az $f^{-1}(x)=f(x)$ típusú egyenleteknél akkor és csak akkor hivatkozhatunk arra, hogy a függvény és inverzének a grafikonja csak az $y=x$ egyenesen metszi egymást, ha ezt az adott egyenlet kapcsán bizonyítottuk.

Létezik-e olyan tétel, amely segítséget nyújt a bizonyításhoz?

Mielőtt erre rátérnénk, oldjuk meg az alábbi feladatot.

7. feladat: Oldjuk meg a valós számok halmazán az alábbi egyenletet:

$\sqrt[3]{4x-3}=\frac{x^3+3}{4}.$

Megoldás: Az könnyen látható, hogy ez az egyenlet is az $f^{-1}(x)=f(x)$ típusú egyenletek közé tartozik, hiszen az $f\colon \mathbb{R}\to \mathbb{R}$; $x\mapsto \sqrt[3]{4x-3}$ és a $g\colon \mathbb{R}\to \mathbb{R}$; $x\mapsto \frac{x^3+3}{4}$ függvények egymás inverzei, ahol mindkét függvény szigorúan monoton növekvő. Átrendezés után az eredetivel ekvivalens $\sqrt[3]{4\cdot \sqrt[3]{4x-3}-3}=x$ egyenletet kapjuk, mely az $f$ függvénnyel kifejezve a következő alakban írható fel: $f\big(f(x)\big)=x$.

Az alábbiakban bebizonyítjuk, hogy mivel az $f$ függvény szigorúan monoton növekedő, azért az $f\big(f(x)\big)=x$ egyenlet megoldáshalmaza megegyezik az $f(x)=x$ egyenlet megoldáshalmazával.

Legyen $z$ megoldása az $f(x)=x$ egyenletnek. Ekkor $f(z)=z$, így $f\big(f(z)\big)= f(z)$, tehát $f\big(f(z)\big)=z$.

Legyen másrészt $r$ megoldása az $f\big(f(x)\big)=x$ egyenletnek, azaz ${f\big(f(r)\big)=r}$. Tegyük fel, hogy $r < f(r)$. Mivel az $f$ függvény szigorúan monoton növekvő, ekkor $f(r) < f\big(f(r)\big)$, tehát $r < f(r) < f\big(f(r)\big)$, ami ellentmondás. Hasonlóan be lehet látni, hogy $f(r) < r$ sem lehetséges, tehát szükségképpen $r=f(r)$. Így a két egyenlet megoldáshalmaza egyenlő.

Tehát az eredeti egyenlet ekvivalens a $\sqrt[3]{4x-3}=x$ egyenlettel. Köbre emelés és átrendezés után $x^3-4x+3=0$. Ennek a megoldásai az eddig alkalmazott módszerek felhasználásával már könnyen meghatározhatók, és ezek az 1, $\frac{-1-\sqrt{13}}{2}$, $\frac{-1+\sqrt{13}}{2}$ számok.

$*$

A feladatnak két nagyon fontos hozadéka a következő.

1. hozadék: Adott az $f^{-1}(x)=f(x)$ egyenlet, ahol $f\colon D_f \to R_f$; $x\mapsto f(x)$ szigorúan monoton növekvő függvény. Ebből következik, hogy $f^{-1}(x)$ is szigorúan monoton növekvő. (Lásd [1], 151. oldal.) Az egyenlet két oldalára alkalmazva a szigorúan monoton $f$ függvényt kapjuk, hogy

$f\big(f^{-1}(x)\big) =f\big(f(x)\big) \quad \Longleftrightarrow \quad x =f\big(f(x)\big).$

Azt pedig az előbb beláttuk, hogy az utolsó egyenlet megoldáshalmaza megegyezik az $f(x)=x$ egyenlet megoldáshalmazával, mivel $f$ szigorúan monoton növekvő. Így az $f^{-1}(x)=f(x)$ egyenlet megoldáshalmaza megegyezik az $f(x)=x$ egyenlet megoldáshalmazával, ha $f$ szigorúan monoton növekvő. Így megfogalmazhatjuk az alábbi tételt.

Tétel. Ha az $f\colon D_f \to R_f$; $x\mapsto f(x)$ függvény szigorúan monoton növekvő, akkor a $D_f \cap R_f$ halmazon az $f^{-1}(x)=f(x)$ egyenlet megoldáshalmaza megegyezik az $f(x)=x$ egyenlet megoldáshalmazával.

Megjegyzés: Az 1. és a 2. feladatra adott első megoldást úgy tehetjük teljesen korrektté, ha belátjuk, hogy az inverz kapcsolatban szereplő függvények szigorúan monoton növekvők. Ezt az olvasóra bízzuk.

2. hozadék: Ha az $f\colon D_f \to R_f$; $x\mapsto f(x)$ függvény szigorúan monoton növekvő, akkor az $\big(f\big(\ldots \big(f(x)\big)\ldots\big)\big) =x$ egyenlet megoldáshalmaza megegyezik az $f(x)=x$ egyenlet megoldáshalmazával.

Végül nézzünk néhány feladatot, melynek megoldását az olvasóra bízzuk.

Oldjuk meg a valós számok halmazán a következő egyenleteket:

1. $\sqrt{x+5} =x^2-5$;

Külön köszönettel tartozom Katz Sándornak, aki értékes tanácsaival segítette munkámat.

Felhasznált irodalom

[1] Laczkovich Miklós – T. Sós Vera: Analízis I. (Nemzeti Tankönyvkiadó, 2006).
[2] Szele Tibor: Bevezetés az algebrába (Tankönyvkiadó, 1972).
[3] Dr. Szendrei János: Algebra és számelmélet (Tankönyvkiadó).
[4] Olosz Ferenc: Egyenletek megoldása inverz függvények felhasználásával.
[5] Szilassi Lajos: A kételkedés joga - és kötelessége.
[4] KöMaL (1893–2010).
[5] NMMV feladatok és megoldások 1992–2007 (CD, Szeged, 2007).