Dinnyék rendezése

A dinnyeárusnak az a mániája, hogy görögdinnyéit, amelyek tökéletesen gömb alakúak, a vízszintes síklapú piaci kőasztalon az asztal hosszában egyenes sorba rakja úgy, hogy a sor belsejében mindegyik dinnye két szomszédjához ér hozzá, és azok a pontok, ahol a dinnyék az asztallaphoz érnek, egy egyenesen helyezkednek el.

Egy reggel, amikor kocsijában tizenegy gömb alakú dinnyével megérkezik a piacra, és még nem rakta ki azokat a maga módján, odamegy hozzá a piaci díjbeszedő és sorra megméri a dinnyék átmérőjét, amelyeket a következőknek talál: d₁=16 cm, d₂=18 cm, d₃=22 cm, d₄=26 cm, d₅=28 cm, d₆=30 cm, d₇=34 cm, d₈=36 cm, d₉=38 cm, d₁₀=40 cm, d₁₁=42 cm. Ezeket összeadja és közli, hogy az árusnak az átmérők összege, vagyis 330 cm után kell helyfoglalási díjat fizetnie. A dinnyeárus ezt nem fogadja el, mondván, hogy ő a dinnyéit az ő mániája szerint ennél rövidebb sorba tudja rendezni az asztalon. Számítsa ki a díjbeszedő a dinnyék méretének ismeretében, hogy milyen hosszú lesz a belőlük összeállítható legrövidebb dinnyesor, s akkor majd annyiért fizet. Erre a díjbeszedő azt mondja, látom, szereti a matematikát; nos jól van, én kiszámítom a legrövidebb dinnyesor hosszát, vagyis annak a síkbeli alakzatnak a kombinatorikus geometriai átmérőjét, amely a megfelelően elrendezett és egymást érintő dinnyék asztalra vett merőleges vetületeinek mint halmazoknak az uniója, ha ön viszont igazolja, hogy ez a hosszúság adott r₁$\displaystyle le$r₂$\displaystyle le$r₃...r_n-1$\displaystyle le$r_n sugarú n darab dinnye esetén akkor a legkisebb, ha a

$\displaystyle D=\left(\sqrt{r_{k_1}}-\sqrt{r_{k_2}}\right)^2+\left(\sqrt{r_{k_2}}-\sqrt{r_{k_3}}\right)^2+\left(\sqrt{r_{k_3}}-\sqrt{r_{k_4}}\right)^2+$

$\displaystyle +\left(\sqrt{r_{k_4}}-\sqrt{r_{k_5}}\right)^2+\dots+\left(\sqrt{r_{k_{n-1}}}-\sqrt{r_{k_n}}\right)^2$

összeg a legnagyobb; ahol tehát r_k1,r_k2,r_k3,...,r_kn-1,r_kn az egyes, egymással érintkező dinnyék gömbsugarát jelöli, és ezen belül k₁,k₂,k₃,...,k_n-1,k_n indexek az 1,2,3,...,n-1,n számok egyik, a minimumot előállító, megfelelő permutációját jelentik. Segítsünk nekik!

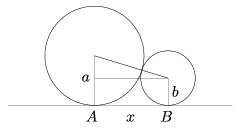
Megoldás: A dinnyesor két szomszédos dinnyéjére az ábra szerint igaz, hogy az asztalon lévő érintkezési pontjaik távolsága $\displaystyle AB=x=2\sqrt{ab}$, ahol a és b a két gömb sugara. Ennek alapján a feladatban meghatározott dinnyesor hossza:

$\displaystyle L=r_{l_1}+2\sqrt{r_{l_1}r_{l_2}}+2\sqrt{r_{l_2}r_{l_3}}+2\sqrt{r_{l_3}r_{l_4}}+2\sqrt{r_{l_{n-1}}r_{l_n}}+r_{l_n},$

ahol r_l1,r_l2,r_l3,...,r_ln,r_ln a dinnyék r₁$\displaystyle le$r₂r₃$\displaystyle le$...$\displaystyle le$r_n-1r_n gömbsugarai valamilyen sorrendben.

A legrövidebb dinnyesorban a dinnyék úgy következnek egymás után, hogy a fenti összeg a legkisebb legyen.

Tekintsük a dinnyék átmérőinek összegét, amely legyen

H=2(r₁+r₂+r₃+r₄+...+r_n1+r_n).

Vonjuk ki a belőle a fentebb kapott L összeget:

2(r₁+r₂+r₃+r₄+...+r_n-1+r_n)-

$\displaystyle -\left(r_{l_1}+2\sqrt{r_{l_1}r_{l_2}}+2\sqrt{r_{l_2}r_{l_3}}+2\sqrt{r_{l_3}r_{l_4}}+\dots+2\sqrt{r_{l_{n-1}}r_{l_n}}+r_{l_n}\right)$

A kisebbítendő tagjait át lehet rendezni abba a sorrendbe, amilyen sorrendben a kivonandóban szerepelnek:

2(r_l1+r_l2+r_l3+...+r_ln1+r_ln)-

$\displaystyle -\left(r_{l_1}+2\sqrt{r_{l_1}r_{l_2}}+2\sqrt{r_{l_2}r_{l_3}}+2\sqrt{r_{l_3}r_{l_4}}+\dots+2\sqrt{r_{l_{n-1}}r_{l_n}}+r_{l_n}\right)$

A kivonás elvégzése utána a maradék:

$\displaystyle D=H-L=r_{l_1}-2\sqrt{r_{l_1}r_{l_2}}+r_{l_2}+r_{l_2}-2\sqrt{r_{l_2}r_{l_3}}+r_{l_3}+r_{l_3}\,-$

$\displaystyle -2\sqrt{r_{l_3}r_{l_4}}+r_{l_4}+\dots+r_{l_{n-1}}-2\sqrt{r_{l_{n-1}}r_{l_n}}+r_{l_n},$

amely viszont a következőképpen írható:

$\displaystyle D=\left(\sqrt{r_{l_1}}-\sqrt{r_{l_2}}\right)^2+\left(\sqrt{r_{l_2}}-\sqrt{r_{l_3}}\right)^2+\left(\sqrt{r_{l_3}}-\sqrt{r_{l_4}}\right)^2+\dots+\left(\sqrt{r_{l_{n-1}}}-\sqrt{r_{l_n}}\right)^2.$

A legrövidebb dinnyesor tehát akkor adódik, ha ez utoljára kapott négyzetösszeg maximális. Ezzel megoldottuk a dinnyeárusra a díjbeszedő által kirótt feladatot.

A díjbeszedő feladatát, vagyis a legrövidebb dinnyesor hosszának megállapítását elvileg úgy oldhatjuk meg, hogy a 11 dinnye minden lehetséges sorrendjét előállítjuk, és megkeressük a legrövidebb sor hosszát. Ennek gyakorlati kivitele hosszadalmas, hiszen 11!=39 916 800 lehetséges sorrendje van a dinnyéknek. A feladatnak ezt a részét is az imént kapott négyzetösszeg útmutatása alapján oldhatjuk meg. Ebben a sugarak négyzetgyökei különbségének négyzetösszege szerepel. Ebből következik, hogy nagy sugarú dinnyék szomszédságában kis sugarúakat kell elhelyezni, amelyre nézve az |r_i-1-r_i|+|r_i-r_i+1| tájékoztató összeg nagyobb számot ad.

Ennek megfelelően tegyük középre a legnagyobb sugarú dinnyét, és tegyük két oldalára a két legkisebb sugarút. Ezek mellé -- kifelé folytatva a sort -- tegyük a következő két legnagyobbat, majd melléjük a következő két legkisebbet, aztán megint a két maradék legnagyobbat, majd a két közepes méretűt a sor két végére; végig figyelve az 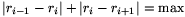kritérium érvényesülésére. Ezzel az eljárással az alábbi sorozathoz jutunk:

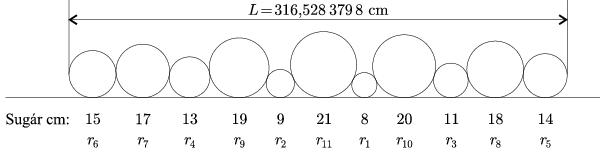
Azaz

l₁=6,   l₂=7,   l₃=4,   l₄=9,   l₅=2,   l₆=11,

l₇=1,   l₈=10,   l₉=3,   l₁₀=8,   l₁₁=5.

$\displaystyle L=r_6+2\bigg(\sqrt{r_6r_7}+\sqrt{r_7r_4}+\sqrt{r_4r_9}+\sqrt{r_9r_2}+\sqrt{r_2r_{11}}+\sqrt{r_{11}r_1}+$

$\displaystyle +\sqrt{r_1r_{10}}+\sqrt{r_{10}r_3}+\sqrt{r_3r_8}+\sqrt{r_8r_5}\bigg)+r_5=316{,}528\;379\;8{\rm\ cm.}$

Ezzel az elrendezéssel az egész dinnyesorra képezett

$\displaystyle Delta$=|r_l1-r_l2|+|r_l2-r_l3|+|r_l3-r_l4|+...+|r_ln-2-r_ln-1|+|r_ln-1-r_ln|

összeg értéke 79; a

$\displaystyle D=\left(\sqrt{r_{l_1}}-\sqrt{r_{l_2}}\right)^2+\left(\sqrt{r_{l_2}}-\sqrt{r_{l_3}}\right)^2+\left(\sqrt{r_{l_3}}-\sqrt{r_{l_4}}\right)^2+\dots+\left(\sqrt{r_{l_{n-1}}}-\sqrt{r_{l_n}}\right)^2$

összeg 13,4716202 cm. Természetesen L+D=H.

Az, hogy a fenti elrendezés a lehetséges legrövidebb sor, az eddigiekből még nem következik. Olvasóinktól várunk egy bizonyítást, vagy egy még rövidebb dinnyesort ....

Légrádi Imre, Sopron