Olimpiai megjegyzések I.
Októberi számunkban közöltük az idei Nemzetközi Matematikai Diákolimpia feladatainak megoldását. Ebben a cikkben az egyik feladatra visszatérve olyan további megoldást mutatunk, amelyik lényegesen különbözik az októberben közölttől, ugyanakkor tanulságos lehet mindazoknak, akik a jövőben országos vagy nemzetközi versenyeken szeretnének eredményesen részt venni. Ebben a megjegyzésben a 2. feladattal foglalkozunk. (Az olimpiai feladatok megoldása a KöMaL 2001/7. számának 389-394. oldalán olvasható.)
A 2. feladat. Bizonyítsuk be, hogy
| (1) | \(\displaystyle {a\over\sqrt{a^2+8bc}}+{b\over\sqrt{b^2+8ca}}+{c\over\sqrt{c^2+8ab}}\ge1\) |
minden a, b, c pozitív valós számra.
A feladat első pillantásra ártalmatlan egyenlőtlenségnek tűnik, ami nem lehet nagyon nehéz... vagy mégis? A magyar csapat számára ez a feladat bizonyult a legnehezebbnek. Hat versenyzőnk együttvéve csupán 2 pontot szerzett meg a lehetséges 42-ből.
A megoldáshoz első lépésként kézenfekvő lehet behelyettesíteni a \(\displaystyle x={bc\over a^2}\), \(\displaystyle y={ca\over b^2}\), \(\displaystyle z={ab\over c^2}\) változókat. Ezek szintén pozitív számok, a szorzatuk 1, és a behelyettesítés után az (1) egyenlőtlenség a következő, egyszerűbb alakot ölti:
| (2) | 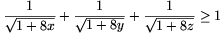 |
Azt is megállapíthatjuk, hogy az x=y=z=1 (azaz a=b=c) esetben egyenlőség áll fenn.
Hogyan tovább? Láthatjuk, hogy a feladat nehézsége abból fakad, hogy összegek négyzetgyökeit kell felülről becsülnünk, ehhez pedig meglehetősen kevés eszköz áll rendelkezésünkre. Ha alsó becslésre volna szükség, akkor egészen más lenne a helyzet. A három négyzetgyökös kifejezést kényelmesen tudjuk alulról becsülni például a számtani és mértani közepek közötti egyenlőtlenséggel. Közben persze vigyáznunk kell, hogy x=y=z=1 esetén mindig egyenlőség álljon:
| (3) | 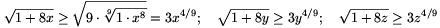 |
Ezek alapján a három gyökös kifejezés szorzatát és összegét sem nehéz alulról megbecsülni.
De mi a helyzet a felső becsléssel? A felső becsléshez jó lenne megszabadulni a kellemetlen négyzetgyökjeltől. Ez pedig legegyszerűbben négyzetre emeléssel lehetséges. Szorozzuk be a (2) egyenlőtlenséget a nevezőkkel. Az így kapott egyenlőtlenségben csupán egyetlen négyzetgyökös kifejezést kell felülről becsülnünk, a jobb oldalt:
| (4) | 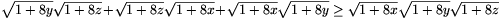 |
Most pedig vegyünk nagy levegőt, emeljük mindkét oldalt négyzetre, és rendezzük az egyenlőtlenséget! (Ne felejtsünk el xyz helyére 1-et írni.) A rendezés után a következő egyenlőtlenséget kapjuk:
| (5) | 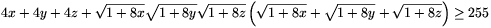 |
A rendezés során azt tapasztaljuk, hogy (4) jobb oldalának négyzetét ,,lenyelik'' a baloldalon álló tagok négyzetei, csupán egy konstans marad.
A megoldás innen kezdve triviális: behelyettesítjük a (3) egyenlőtlenség-hármast és alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget.
Kós Géza

