Olimpiai megjegyzések II.
Az első részben az idei Nemzetközi Matematikai Diákolimpia 2. feladatára mutattunk egy lehetséges megoldást. Most a 6. feladatot vizsgáljuk meg közelebbről. A feladatra két megoldást is mutatunk.
Az első -- hasonlóan a 2. feladat megoldásához -- nem használ semmilyen különleges ötletet vagy a középiskolai anyagon túlmutató ismeretet. Viszont egy olyan lépéssel kezdődik, amely első pillantásra talán túl ijesztő lehet.
A második megoldás jóval több ismeretet igényel. Ez a megoldás az egész számok halmazának egy kiterjesztése, az úgynevezett Euler-egészek elméletét használja fel. Cserébe viszont megmutatja a feladat valószínű eredetét.
A 6. feladat. Legyenek a, b, c, d egészek, amelyekre a>b>c>d>0. Tegyük fel, hogy
| (6) | ac+bd=(b+d+a-c)(b+d-a+c). |
Bizonyítsuk be, hogy ab+cd nem prímszám.
A (6) egyenletet átrendezve,
| (7) | a2-ac+c2=b2+bd+d2. |
A továbbiakban mindig ezt az alakot fogjuk használni.
1. megoldás: Helyettesítsünk be!
A megoldás indirekt. Feltételezzük, hogy ab+cd=p, ahol p egy prímszám. Ezzel már egy egész egyenletrendszerünk van:
| (8) | a2-ac+c2=b2+bd+d2, ab+cd=p. |
Az ismeretlenek és az egyenletek számát úgy csökkenthetjük, hogy az egyik egyenletből kifejezünk egy alkalmas kifejezést, és behelyettesítjük a másik egyenletbe. Hogy mindez még kényelmesebb legyen, először csak modulo p fogunk számolni.
A második egyenlet szerint 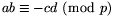 . Szorozzuk meg a (7)
egyenletet b2-tel, és helyettesítsünk be ab
helyére (-cd)-t:
. Szorozzuk meg a (7)
egyenletet b2-tel, és helyettesítsünk be ab
helyére (-cd)-t:
0=b2(b2+bd+d2-a2+ac-c2)=b4+b3d+b2d2-(ab)2+ab.bc-b2c2
 b4+b3d+b2d2-(cd)2-cd.bc-b2c2=(b+c)(b-c)(b2+bd+d2)
(mod p).
b4+b3d+b2d2-(cd)2-cd.bc-b2c2=(b+c)(b-c)(b2+bd+d2)
(mod p).
A behelyettesítés nyomán kapott kifejezés három tényező szorzatára bomlik, és ezek egyike éppen a (7) egyenletben szereplő mennyiség.
A kapott kongruencia szerint az utolsó három tényező: b+c, b-c és b2+bd+d2 valamelyike osztható p-vel, hiszen feltevésünk szerint p prímszám. A b+c és b-c számok pozitívak és kisebbek, mint ab+cd=p, ezért nem lehetnek p-vel oszthatók; marad az az eset, hogy b2+bd+d2 osztható p-vel. Mivel
0<b2+bd+d2<ab+ab+cd<2(ab+cd)=2p,
a b2+bd+d2 szám csak úgy lehet p-vel osztható, ha egyenlő vele. Ezzel a következtetéssel az egyenletrendszer a következőképpen alakul:
| (9) | a2-ac+c2=b2+bd+d2=ab+cd=p. |
Ebből már nem nehéz ellentmondásra jutni. Ha a (9) egyenletet modulo a vizsgáljuk (az ismeretlenek között az a a legnagyobb), láthatjuk, hogy c(c-d)=ab+ac-a2 osztható a-val. Mivel azonban a és c relatív prímek -- másképpen ab+cd nem lenne prímszám -- és 0<c-d<a, ez nem lehetséges.
2. megoldás az Euler-egészek felől
Aki olvasott már az Euler-egészekről, az a (7) egyenletre nézve azonnal sejtheti, hogy ez a feladat szorosan kapcsolódik hozzájuk.
Legyen  az egyik komplex harmadik egységgyök. Az
x+y
az egyik komplex harmadik egységgyök. Az
x+y alakú komplex számokat, ahol x és y
egész számok, Euler-egészeknek nevezzük. Az Euler-egészek a
komplex számsíkon szabályos háromszögrácsot alkotnak (1. ábra).
alakú komplex számokat, ahol x és y
egész számok, Euler-egészeknek nevezzük. Az Euler-egészek a
komplex számsíkon szabályos háromszögrácsot alkotnak (1. ábra).
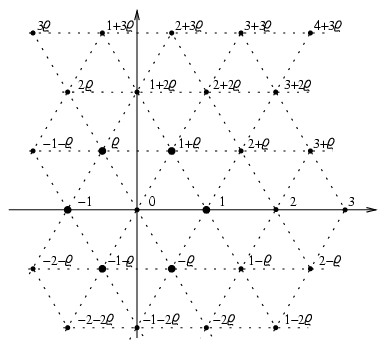
1. ábra
Ennek a számhalmaznak nagyon sok érdekes és hasznos számelméleti tulajdonsága van. Ezek segítségével bizonyította be annak idején Leonhard Euler a Fermat-sejtést a 3-as kitevőre. Akit a téma részletesebben érdekel, annak Turán Pál--Gyarmati Edit: Bevezetés a számelméletbe című jegyzetét ajánljuk. Most csak röviden foglaljuk össze az Euler-egészekkel kapcsolatos, a megoldáshoz szükséges legfontosabb fogalmakat és tételeket.
Az Euler-egészek körében is értelmezzük az összeadást, a kivonást
és a szorzást. Ezeket teljesen természetes módon definiáljuk, a
szorzásnál figyelembe véve, hogy  2=-
2=- -1:
-1:
\(\displaystyle \displaylines{(x+y\varrho)\pm(u+v\varrho)=(x\pm u)+(y\pm v)\varrho;\cr(x+y\varrho)(u+v\varrho)=xu+(xv+yu)\varrho+yv\varrho^2=(xu-yv)+(xv+uy-yv)\varrho.\cr}\)
Az összeadásnak és a szorzásnak az egész vagy a valós számok esetében megszokott kommutatív, asszociatív és disztributív tulajdonságai az Euler-egészek körében is igazak. Ugyancsak fennállnak a 0 és az 1 számok alapvető tulajdonságai, például bármelyik Euler-egészhez 0-t adva magát a számot kapjuk eredményül, vagy minden Euler-egész 0-szorosa a 0.
Az  =x+y
=x+y Euler-egész konjugáltja az
Euler-egész konjugáltja az
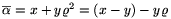 szám.
szám.
Egy nagyon fontos mennyiség az Euler-egészek normája. Az
 =x+y
=x+y Euler-egész normáját N(
Euler-egész normáját N( )-val jelöljük
és a következőképpen definiáljuk:
)-val jelöljük
és a következőképpen definiáljuk:
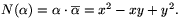
A norma mindig nemnegatív egész szám, és csak a 0 normája 0.
A norma nem más, mint a komplex értelemben vett abszolút érték négyzete. Ebből is következik, hogy szorzat normája a tényezők normáinak szorzata:
N( .
. )=N(
)=N( ).N(
).N( ).
).
Az  Euler-egész osztója a
Euler-egész osztója a  Euler-egésznek, ha létezik olyan
Euler-egésznek, ha létezik olyan  Euler-egész,
amelyre
Euler-egész,
amelyre 
 =
= . A norma multiplikativitása miatt igaz, hogy ha
. A norma multiplikativitása miatt igaz, hogy ha  |
| , akkor
N(
, akkor
N( )|N(
)|N( ). (Az utóbbi oszthatóság a racionális egész számok körében
értendő.)
). (Az utóbbi oszthatóság a racionális egész számok körében
értendő.)
Hat olyan Euler-egész van, amelynek a normája 1. Ezeket egységeknek nevezzük és az 1. ábrán kiemeltük. Az egységek minden Euler-egésznek osztói.
Két Euler-egészt asszociáltnak nevezünk, ha egymás egységszeresei, vagyis egymásból a 0 körüli, a 60o többszörösével történő forgatással kaphatók.
Egy egységtől különböző  Euler-egészt felbonthatatlannak,
idegen szóval irreducibilisnek nevezünk, ha csak az egységekkel
és a saját asszociáltjaival osztható.
Euler-egészt felbonthatatlannak,
idegen szóval irreducibilisnek nevezünk, ha csak az egységekkel
és a saját asszociáltjaival osztható.
Egy egységtől és 0-tól különböző  Euler-egészt prímnek nevezünk, ha
tetszőleges
Euler-egészt prímnek nevezünk, ha
tetszőleges  ,
,  Euler-egészek esetén, ha
Euler-egészek esetén, ha  |
|
 , akkor
, akkor  |
| vagy
vagy  |
| . A továbbiakban, hogy megkülönböztessük
az Euler-egészek körében prím számokat a valós prímszámoktól, az
előbbieket Euler-prímeknek fogjuk hívni.
. A továbbiakban, hogy megkülönböztessük
az Euler-egészek körében prím számokat a valós prímszámoktól, az
előbbieket Euler-prímeknek fogjuk hívni.
Az Euler-egészek számelméletének legalapvetőbb tételei a következők:
1. A felbonthatatlan Euler-egészek és az Euler-prímek ugyanazok.
2. Az Euler-egészek körében is igaz a számelmélet alaptétele. Minden 0-tól és egységtől különböző Euler-egész az asszociáltságtól eltekintve egyféleképpen írható fel Euler-prímek és egységek szorzataként, azaz két tetszőleges felírásban a megfelelő prímtényezők egymás asszociáltjai.
3. A 3k+2 alakú prímszámok egyben Euler-prímek is. A
3k+1 alakú prímszámok felbomlanak két konjugált, egymással nem
asszociált Euler-prím szorzatára (pl. 7=(3+ )(2-
)(2- )). A 3
prímtényezős felbontása pedig 3=-
)). A 3
prímtényezős felbontása pedig 3=- 2(1-
2(1- )2.
)2.
A tételekből látható, hogy egy  Euler-egész prímtényezős felbontása és
N(
Euler-egész prímtényezős felbontása és
N( )
prímtényezős felbontása között szoros kapcsolat van. Az
)
prímtényezős felbontása között szoros kapcsolat van. Az  minden egyes
3k+2 alakú prímtényezőjének négyzete szerepel az N(
minden egyes
3k+2 alakú prímtényezőjének négyzete szerepel az N( )
felbontásában, a további prímtényezőknek pedig a normája, ami vagy 3,
vagy pedig egy-egy 3k+1 alakú prímszám.
)
felbontásában, a további prímtényezőknek pedig a normája, ami vagy 3,
vagy pedig egy-egy 3k+1 alakú prímszám.
Például az  =10+8
=10+8 Euler-egész prímtényezős felbontása 2.(2+
Euler-egész prímtényezős felbontása 2.(2+ )(3+
)(3+ ), normájáé
pedig N(
), normájáé
pedig N( )=N(2).N(2+
)=N(2).N(2+ ).N(3+
).N(3+ )=22.3.7.
)=22.3.7.
Megfordítva, N( ) prímtényezős felbontása ,,majdnem
egyértelműen'' meghatározza
) prímtényezős felbontása ,,majdnem
egyértelműen'' meghatározza  prímtényezős felbontását. Az
N(
prímtényezős felbontását. Az
N( )
minden 3k+2 alakú prímosztója
)
minden 3k+2 alakú prímosztója  -nak is prímosztója (feleakkora
kitevővel), és N(
-nak is prímosztója (feleakkora
kitevővel), és N( ) felbontásában minden egyes 3-as
tényező az 1-
) felbontásában minden egyes 3-as
tényező az 1- Euler-prím normája. Az N(
Euler-prím normája. Az N( ) 3k+1
alakú prímosztói is
) 3k+1
alakú prímosztói is  egy-egy prímosztójának normái, de ez a prímosztó -- az
asszociáltságtól eltekintve is -- kétféle lehet.
egy-egy prímosztójának normái, de ez a prímosztó -- az
asszociáltságtól eltekintve is -- kétféle lehet.
Visszatérve a feladathoz, legyen  =a+c
=a+c és
és  =b-d
=b-d . A feltétel szerint
a2-ac+c2=b2+bd+d2,
azaz N(
. A feltétel szerint
a2-ac+c2=b2+bd+d2,
azaz N( )=N(
)=N( ); a bizonyítandó állítás pedig az, hogy
ab+cd, ami nem más, mint
); a bizonyítandó állítás pedig az, hogy
ab+cd, ami nem más, mint 
 =(ab+cd)+(bc+cd-ad)
=(ab+cd)+(bc+cd-ad) ,,valós
része'', nem lehet prímszám.
,,valós
része'', nem lehet prímszám.
Mivel N( )=N(
)=N( ), a két szám Euler-prímtényezős felbontása ,,majdnem'' ugyanaz. A prímosztók egy része közös, a további prímtényezők pedig egymás konjugáltjai a két felbontásban. Formálisan felírva,
), a két szám Euler-prímtényezős felbontása ,,majdnem'' ugyanaz. A prímosztók egy része közös, a további prímtényezők pedig egymás konjugáltjai a két felbontásban. Formálisan felírva,
| (10) | 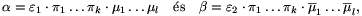 |
ahol  1, ...,
1, ...,  k és
k és  1, ...,
1, ...,
 l Euler-prímek,
l Euler-prímek,  1 és
1 és  2 pedig egységek.
2 pedig egységek.
Legyen  =
= 1.....
1..... k
és
k
és  =
= 1.....
1..... l;
a fentiek szerint ekkor
l;
a fentiek szerint ekkor
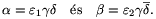
(Előfordulhat, hogy a két felbontásban csak közös vagy csak
konjugált prímtényezők szerepelnek; ezekben az esetekben  =1, illetve
=1, illetve
 =1.)
=1.)
Vizsgáljuk most az
| (11) |   =(ab+cd)+(bc+cd-ad) =(ab+cd)+(bc+cd-ad) = = 1 1 2 2 2.N( 2.N( ) ) |
számot. Ez a szám osztható N( )-val; ebből következik, hogy
ab+cd és bc+cd-ad is osztható
N(
)-val; ebből következik, hogy
ab+cd és bc+cd-ad is osztható
N( )-val. Már csak az hiányzik a bizonyítás befejezéséhez,
hogy sem N(
)-val. Már csak az hiányzik a bizonyítás befejezéséhez,
hogy sem N( )=1, sem ab+cd=N(
)=1, sem ab+cd=N( ) nem
lehetséges.
) nem
lehetséges.
Ha N( )=1, azaz
)=1, azaz  =1, akkor
=1, akkor  és
és  asszociáltak, vagyis 0 körüli, valahányszor
60o-os elforgatottjai egymásnak. Azt, hogy az elforgatás
pontosan hányszor 60o-os, az
asszociáltak, vagyis 0 körüli, valahányszor
60o-os elforgatottjai egymásnak. Azt, hogy az elforgatás
pontosan hányszor 60o-os, az  és
és  argumentumának vizsgálatával dönthető
el.
argumentumának vizsgálatával dönthető
el.
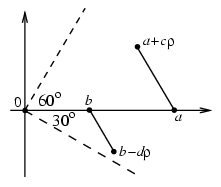
2. ábra
Az a>b>c>d>0 feltételből
következik, hogy  argumentuma 0o és 60o között,
argumentuma 0o és 60o között,  argumentuma
pedig -30o és 0o között van (2. ábra). A
két szám argumentumának különbsége tehát 0 és 90o közé
esik, az elforgatás szöge pontosan 60o, azaz
argumentuma
pedig -30o és 0o között van (2. ábra). A
két szám argumentumának különbsége tehát 0 és 90o közé
esik, az elforgatás szöge pontosan 60o, azaz  =(1+
=(1+ )
) . Ebben az
esetben viszont
. Ebben az
esetben viszont
 =a+c
=a+c =(1+
=(1+ )(b-d
)(b-d )=(b+d)+b
)=(b+d)+b ,
,
ami nem lehetséges, mert b>c. Az N( )=1 feltevés
tehát ellentmondásra vezet.
)=1 feltevés
tehát ellentmondásra vezet.
Ha ab+cd=N( ), akkor a (11) egyenletet N(
), akkor a (11) egyenletet N( )-val osztva,
)-val osztva,
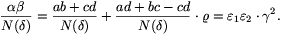
Ez a szám, mint a jobb oldal mutatja, egy Euler-egész. Az
argumentuma  és
és  argumentumának öszege, tehát -30o és
60o közé esik, a ,,valós része'' pedig a feltevés szerint
argumentumának öszege, tehát -30o és
60o közé esik, a ,,valós része'' pedig a feltevés szerint
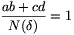 . Az egyetlen ilyen Euler-egész az 1 (3. ábra),
tehát
. Az egyetlen ilyen Euler-egész az 1 (3. ábra),
tehát  1
1 2
2 2=1
és
2=1
és 
 =N(
=N( ).
).
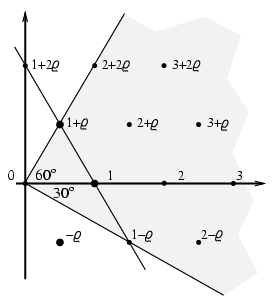
3. ábra
Az  és
és
 számok
szorzata tehát az N(
számok
szorzata tehát az N( ) valós pozitív szám. Mivel
N(
) valós pozitív szám. Mivel
N( )=N(
)=N( ), ebből következik, hogy a két szám egymás
konjugáltja. Ekkor azonban
), ebből következik, hogy a két szám egymás
konjugáltja. Ekkor azonban
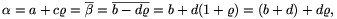
ami nem lehetséges, mert c>d. Tehát az
ab+cd=N( ) feltevés is ellentmondásra
vezet. Ezzel az állítást igazoltuk.
) feltevés is ellentmondásra
vezet. Ezzel az állítást igazoltuk.
A második megoldás nem csupán bebizonyítja a feladat állítását,
hanem egy eljárást is ad olyan a,b,c,d
számnégyesek keresésére, amelyekre
a>b>c>d és
a2-ac+c2=b2+bd+d2. Csupán
megfelelő argumentumú  és
és  Euler-egészeket kell választanunk.
Euler-egészeket kell választanunk.
Például az
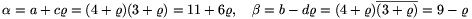
választással a=11, b=9, c=6 és d=1, továbbá a2-ac+c2=b2+bd+d2=91. (Természetesen ab+cd=105 nem prím.)
Kós Géza

