Minden háromszög egyenlő szárú

Húzzuk meg az ABC háromszög C-ből induló szögfelezőjét és az AB oldal felező merőlegesét. Ha AC és BC egyenlő, akkor kész vagyunk. Ha nem, akkor a szögfelező és a felező merőleges nem lehetnek sem párhuzamosak, sem egybeesők, tehát metszik egymást. Legyen M a metszéspontjuk.

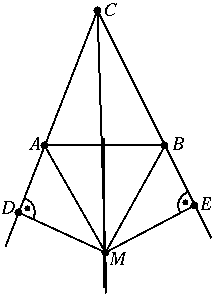
Állítsunk merőlegest M-ből az AC és BC oldalak meghosszabbítására; legyen ezek talppontja D illetve E.

A CMD és CME háromszögek egybevágóak, mivel M a szögfelezőn van. Ezért CD=CE és DM=EM. Másrészt AM=BM, mert M a felezőmerőlegesen is rajta van.

Az ADM és BEM derékszögű háromszögek egybevágóak, mert - mint láttuk - átfogóik ugyanakkorák, és a DM és EM befogók hossza is megegyezik. Ezért a másik befogójuk is ugyanakkora: AD=BE.

MIndezekből következik, hogy

AC=CD-AD=CE-BE=BC.

Könnyű ellenőrizni, hogy a bizonyítás akkor is működik, ha az M pont a háromszög belsejében van.