Az A. 390. feladat (2006. január)

A. 390. Határozzuk meg az összes olyan $f\colon \mathbb{R}\to\mathbb{R}$ függvényt, amelyre

(f(x)+f(y))(f(z)+1)=f(xz-y)+f(x+yz)

teljesül tetszőleges x, y, z valós számok esetén.

(5 pont)

A beküldési határidő 2006. február 15-én LEJÁRT.

Paulin Roland megoldása.

(f(x)+f(y))(f(z)+1)=f(xz-y)+f(x+yz)

(1)

Az f(x)=0 függvény megoldás, hiszen erre (1) mindkét oldalán 0 áll. Feltesszük, hogy f(x) olyan megoldás, amely nem azonosan 0. Helyettesítsünk (1)-be x=y=0-t: 2f(0)(f(z)+1)=2f(0) $\to$ f(0)f(z)=0. Mivel $\exists$ z: f(z) $\ne$ 0, ezért

f(0)=0.

(2)

(1)-be z=0-t helyettesítünk, és használjuk (2)-t: f(x)+f(y)=f(-y)+f(x), így

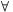$\forall$ y: f(-y)=f(y).

(3)

Helyettesítsünk (1)-be y=0-t: f(x)(f(z)+1)=f(xz)+f(x), így

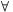$\forall$ x,z: f(x)f(z)=f(xz).

(4)

(4)-be z=1-et helyettesítünk, és olyan x-et veszünk, melyre f(x) $\ne$ 0: f(x)f(1)=f(x) $\to$ f(1)=1. n-re vonatkozó teljes indukcióval belátjuk, hogy minden egész n-re f(n)=n². n=0-ra és n=1-re az állítás igaz. Tegyük fel, hogy az állítás igaz 0, 1, 2,..., N-re, ahol N $\ge$ 1. Helyettesítsünk (1)-be x=N, y=z=1-et: (f(N)+f(1))(f(1)+1)=f(N-1)+f(N+1) $\to$ 2(N²+1)=(N-1)²+f(N+1) $\to$ f(N+1)=(N+1)². Ezzel minden nemnegatív egészre beláttuk az állítást. Ha n<0, akkor (3) miatt f(n)=f(-n)=(-n)²=n², így az állítás igaz.

Legyen $r=\frac uv$ egy tetszőleges racionális szám (v $\ne$ 0). (4) miatt $f(r)f(v)=f(u) \to f(r)v^2=u^2 \to f(r)=\Big(\frac uv\Big)^2$ , így

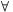$\forall$ r $\in$ Q: f(r)=r².

(5)

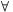(3) és (4) alapján f(x)=f(|x|)=f(sqrt|x|)² $\ge$ 0 minden x-re. Helyettesítsünk (1)-be x=1, z=y-t: (1+f(y))(f(y)+1)=f(0)+f(1+y²) $\to$ f(1+y²)=(1+f(y))² $\ge$ 1, hiszen f(y) $\ge$ 0. Mivel minden a $\ge$ 1 szám előáll a=1+y² alakban, ezért $\forall$ a $\ge$ 1: f(a) $\ge$ 1. Ha 0<x<y, akkor (4) és az előbbiek alapján $f(y)=f\Big(x\cdot \frac yx\Big)=f(x)f\Big(\frac yx\Big)\ge f(x)$ , hiszen f(x) $\ge$ 0 és $f\Big(\frac yx\Big)\ge1$ . Tehát f(x) függvény a (0, 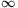$\infty$ ) intervallumon monoton nő. Rögzített x>0 esetén tetszőleges 0< $\varepsilon$ <x-re található olyan p és q racionális szám, melyekre 0<x- $\varepsilon$ <p<x<q<x+ $\varepsilon$ , és így a monotonitás és (5) miatt (x- $\varepsilon$ )²<p²=f(p) $\le$ f(x) $\le$ f(q)=q²<(x+ $\varepsilon$ )². 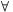Mivel $\lim_{\varepsilon\to0}{(x-\varepsilon)^2}= \lim_{\varepsilon\to0}{(x+\varepsilon)^2}=x^2$ , ezért x² $\le$ f(x) $\le$ x², vagyis $\forall$ x>0: f(x)=x². x<0-ra f(x)=f(-x)=(-x)²=x², míg x=0-ra f(0)=0=0², tehát f(x)=x² minden x-re.

Ez a függvény valóban megoldása a függvényegyenletnek: (x²+y²)(z²+1)=(xz-y)²+(x+yz)², hiszen kibontva a zárójeleket ezzel ekvivalens az x²z²+y²z²+x²+y²=x²z²-2xyz+y²+x²+2xyz+y²z² azonosság. Tehát 2 megoldás van: az f(x)=0 és az f(x)=x².

Statisztika:

14 dolgozat érkezett.

5 pontot kapott: Estélyi István, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Komáromy Dani, Kónya 495 Gábor, Nagy 224 Csaba, Paulin Roland, Tomon István.

4 pontot kapott: Erdélyi Márton, Kutas Péter.

2 pontot kapott: 2 versenyző.

A KöMaL 2006. januári matematika feladatai

14 dolgozat érkezett.
5 pontot kapott:	Estélyi István, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Komáromy Dani, Kónya 495 Gábor, Nagy 224 Csaba, Paulin Roland, Tomon István.
4 pontot kapott:	Erdélyi Márton, Kutas Péter.
2 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?