 |
Az A. 398. feladat (2006. április) |
A. 398. Adott a síkon egy k kör, a körön kívül fekvő 
egyenes, továbbá a körön egy O pont.
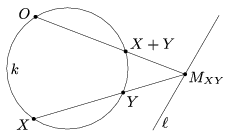
Definiáljuk a k kör pontjain a + kétváltozós műveletet a következőképpen. A kör bármely X, Y pontpárjára jelöljük MXY-nal és az XY egyenes metszéspontját. (Ha X=Y, akkor az XY egyenes az érintő. Ha a két egyenes párhuzamos, akkor MXY az ideális pontja.) Szerkesszük meg az OMXY egyenes és a kör másik metszéspontját. (Ha OMXY érinti a kört, akkor a másik metszéspont is O.) Ez a pont legyen X+Y.
Mutassuk meg, hogy a + művelet kiterjeszthető a k kör és az egyenes összes, valamint ideális pontjára úgy, hogy a pontok a + művelettel kommutatív csoportot alkossanak, amelynek egységeleme az O pont, azaz teljesüljenek a következő feltételek:
a) Tetszőleges X, Y, Z-re (X+Y)+Z=X+(Y+Z);
b) Tetszőleges X, Y esetén X+Y=Y+X;
c) Tetszőleges X-re X+O=X;
d) Tetszőleges X-hez létezik olyan Y, amelyre X+Y=O.
(5 pont)
A beküldési határidő 2006. május 18-án LEJÁRT.
Statisztika:
9 dolgozat érkezett. 5 pontot kapott: Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Nagy 224 Csaba, Paulin Roland, Tomon István. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2006. áprilisi matematika feladatai