 |
Az A. 517. feladat (2010. október) |
A. 517. Legyen m 3 egész szám, és legyen
3 egész szám, és legyen 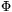 m(x) az m-edik körosztási polinom, továbbá legyen
m(x) az m-edik körosztási polinom, továbbá legyen 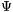 m(x) az az egész együtthatós polinom, amelyre
m(x) az az egész együtthatós polinom, amelyre
Igazoljuk, hogy tetszőleges a egész számra a 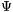 m(a) szám minden prímosztója vagy osztója m-nek, vagy pedig mk
m(a) szám minden prímosztója vagy osztója m-nek, vagy pedig mk 1 alakú.
1 alakú.
(A körosztási polinomokról és a 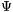 m polinomról bővebben olvashatunk Keith Kearnes, Kiss Emil és Szendrei Ágnes Gauss egészek és Dirichlet tétele c. cikkében, a KöMaL 2010. márciusi és áprilisi számaiban.)
m polinomról bővebben olvashatunk Keith Kearnes, Kiss Emil és Szendrei Ágnes Gauss egészek és Dirichlet tétele c. cikkében, a KöMaL 2010. márciusi és áprilisi számaiban.)
(5 pont)
A beküldési határidő 2010. november 10-én LEJÁRT.
Statisztika:
5 dolgozat érkezett. 5 pontot kapott: Backhausz Tibor. 4 pontot kapott: Ágoston Tamás, Nagy 235 János, Nagy 648 Donát. 3 pontot kapott: 1 versenyző.
A KöMaL 2010. októberi matematika feladatai

