Az A. 574. feladat (2012. november)

A. 574. Legyen n $\ge$ 2, és legyen $p(x)=x^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$ valós együtthatós polinom.

Bizonyítsuk be, hogy ha valamilyen pozitív egész k-ra p(x) osztható a (x-1)^k+1 polinommal, akkor

$\sum_{\ell=0}^{n-1} |a_\ell| > 1+\frac{2k^2}{n}.$

CIIM 2012 (Guanajuato, Mexikó)

(5 pont)

A beküldési határidő 2012. december 10-én LEJÁRT.

Megoldásvázlat. Definiáljuk a_n=1-et is.

Lemma. Tetszőleges, legfeljebb k-adfokú q(y) polinomra $\sum\limits_{\ell=0}^n a_\ell \, q(\ell) = 0$ .

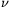
Bizonyítás. Legyen $\varphi$ ₀(y)=1, és legyen $\varphi_\nu(y)=y(y-1)\ldots(y-\nu+1)$ minden $\nu=1,2,\ldots$ esetén. Mivel (x-1)^k|p(x), minden 0 $\le$ $\nu$ $\le$ k-ra

$\sum_{\ell=0}^n a_\ell \, \varphi_\nu(\ell) = p^{(\nu)}(1) = 0,$

ahol $p^{(\nu)}$ a p polinom 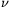$\nu$ -edik deriváltját jelenti. Minden, legfeljebb k-adfokú polinom előáll a $\varphi_0(y),\ldots,\varphi_k(y)$ polinomok lineáris kombinációjaként, tehát $q(y)=\sum\limits_{\nu=0}^k c_\nu \varphi_\nu(y)$ alkalmas $c_0,\ldots,c_k$ valós számokkal. Ezért

$\sum_{\ell=0}^n a_\ell \, q(\ell) = \sum_{\ell=0}^n a_\ell \left( \sum_{\nu=0}^k c_\nu \, \varphi_\nu(\ell) \right) = \sum_{\nu=0}^k c_\nu \left( \sum_{\ell=0}^n a_\ell \, \varphi_\nu(\ell) \right) = 0.$

A lemmát egy olyan q polimomra fogjuk alkalmazni, amelyre q(0),q(1),...,q(n-1) kicsi, és hozzájuk képest q(n) nagy. A q megkonstruálásához a T_k Csebisev-polinomot fogjuk használni, amire T_k(cos t)=cos (kt). A |T_k(x)| értéke a [-1,1] intervallumban mindenhol legfeljebb 1, de az 1 közelében már nagyon gyosan nő.

Legyen

$q(y) = T_k\left(\frac2{n-1}y-1\right).$

Ekkor $q(0),\ldots,q(n-1)\in T_k\big([-1,1]\big)=[-1,1]$ .

Könnyen ellenőrizhető, hogy

$T_k'(1) = \lim_{x\to 1-0} \frac{1-T_k(x)}{1-x} = \lim_{t\to 0} \frac{1-\cos (kt)}{1-\cos t} = \lim_{t\to 0} \frac{2\sin^2(kt/2)}{2\sin^2(t/2)} = \lim_{t\to 0} \left(k^2\bigg(\frac{\frac{\sin(kt/2)}{kt/2}}{\frac{\sin(t/2)}{t/2}}\bigg)^2\right) = k^2.$

A T_k polinom főegyütthatója pozitív, és mind a k gyöke a (-1,1) intervallumban van, ezért a polinom az [1,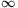 $\infty$ ) intervallumban szigorúan konvex. Ebből következik hogy

$q(n) = T_k\left(1+\frac2{n-1}\right) > T_k(1) + T_k'(1)\frac2{n-1} = 1+\frac{2k^2}{n-1} > 1+\frac{2k^2}{n}.$

Ezek után a Lemmát alkalmazva,

$\sum_{\ell=0}^{n-1} |a_\ell| \ge \sum_{\ell=0}^{n-1} a_\ell\big(-q(\ell)\big) = q(n) > 1+\frac{2k^2}{n}.$

Statisztika:

3 dolgozat érkezett.

5 pontot kapott: Ioan Laurentiu Ploscaru.

1 pontot kapott: 2 versenyző.

A KöMaL 2012. novemberi matematika feladatai

3 dolgozat érkezett.
5 pontot kapott:	Ioan Laurentiu Ploscaru.
1 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?