Az A. 588. feladat (2013. április)

A. 588. Legyen a pozitív egész. Bizonyítsuk be, hogy 7a²(a+1)-1 minden prímosztója 7k $\pm$ 1 alakú.

(5 pont)

A beküldési határidő 2013. május 10-én LEJÁRT.

Megoldásvázlat. Az 15²=225-nél kisebb prímekre az állítás (kezelhetően) véges sok eset vizsgálatával igazolható.

A nagyobb prímekre végtelen leszállással bizonyítunk. Tegyük fel, hogy van olyan p>225 prímszám, ami nem 7k $\pm$ 1 alakú, és olyan a egész, amikre p osztója (7a²(a+1)-1)-nek. Vegyük a legkisebb ilyen p prímet, és hozzá egy alkalmas a-t.

I. Első lépésként keressünk olyan n és b egészeket, amikre $b\equiv na\pmod{p}$ , $1\le n<\sqrt{p}$ és $|b|<\sqrt{p}$ . Legyen $N=\big[\sqrt{p}\big]$ , és helyezzük el a 0,a,2a,...,Na modulo p maradékosztályokat egy p hosszú kör mentén. Ezek a kört N+1 ívre osztják, ezért biztosan van az ívek között legfeljebb $\frac{p}{N+1}<\sqrt{p}$ hosszúságú; valamelyik két 0 $\le$ i<j $\le$ N indexre az ia és ja pontok távolsága kisebb, mint $\sqrt{p}$ . Legyen n=j-i és b $\equiv$ na=(ja-ia); ekkor tehát $|b|<\sqrt{p}$ .

Ha b-nek és n-nek van egy d>1 közös osztója, akkor cseréljük ki őket a b/d és n/d számokra; ezután azt is feltehetjük, hogy b és n relatív prímek.

II. Most legyen A=7b³+7b²n-n³. Ekkor

$A \equiv 7(na)^3+7(na)^2n-n^3 = n^3(7a^3+7a^2-1) \equiv 0 \pmod{p},$

azaz A osztható p-vel, továbbá triviálisan

|A|<15p^3/2<p².

A 7-tel nem osztható köbszámok $\pm$ 1 maradékot adnak 7-tel osztva. Ha n nem osztható 7-tel, akkor tehát $A\equiv -n^3\equiv\pm1\pmod7$ . Ezért A-nak kell, hogy legyen még legalább egy olyan q prímosztója, ami nem 7, és nem is 7k $\pm$ 1 alakú.

Ha n osztható 7-tel, n=7m, akkor b nem osztható 7-tel. Ilyenkor az $\frac{A}7=b^3+7b^2m-49m^3$ szám lesz 7k $\pm$ 1 alakú, és ilyenkor is létezik p-kívül még egy q prímszosztója az A/7-nek, ami nem 7, és nem is 7k $\pm$ 1 alakú.

A q szám kisebb, mint p, mert pq|A, és így

$q \le \frac{A}{p} < \frac{p^2}{p} = p.$

III. Végül, mivel b és n relatív prímek, egyikük sem lehet osztható q-val. Legyen n^-1 az n multiplikatív inverze modulo q, és legyen c=n^-1b. Ekkor

$7c^3+7c^2-1 \equiv n^{-3}(7b^3+7b^2n-n^3) \equiv 0 \pmod{q}.$

Ez pedig azt jelenti, hogy találtunk egy p-nél kisebb ,,rossz'' prímet, a q-t. Ez ellentmond annak, hogy a lehető legkisebb p-t vettük.

Megjegyzés. A feladat kapcsolódik Keith Kearnes, Kiss Emil és Szendrei Ágnes Gauss egészek és Dirichlet tétele c. cikkéhez (KöMaL 2010/3-4) és az A. 517. feladathoz. A cikk (valamivel mélyebb eszközöket használva) lényegesen általánosabb, közvetlen megoldást ad a feladatra.

A cikk jelöléseivel

$\frac{\Phi_7(x)}{x^3} = x^3+x^2+x+1+\frac1x+\frac1{x^2}+\frac1{x^3} = \left(x+\frac1x\right)^3+\left(x+\frac1x\right)^2-2\left(x+\frac1x\right)-1$

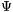$\Psi$ ₇(x)=x³+x²-2x-1

$7a^3+7a^2b-b^3 = (a+b)^3\Psi_7\left(\frac{2a+b}{a+b}\right).$

Relatív prím a,b számok esetén ennek a kifejezésnek minden prímosztója 7, vagy 7k $\pm$ 1 alakú.

Statisztika:

1 dolgozat érkezett.

0 pontot kapott: 1 versenyző.

A KöMaL 2013. áprilisi matematika feladatai

Már regisztráltál?
Új vendég vagy?