Az A. 601. feladat (2013. november)

A. 601. Legyen q1 egész szám. Bizonyítsuk be, hogy van olyan C_q egész szám, hogy minden egész számokból álló véges A halmazra

|A+q^.A|(q+1)|A|-C_q.

(Az A+q^.A halmaz azon egész számokból áll, melyek felírhatók a+qa' alakban alkalmas a,a'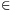A-val.)

(Schweitzer-verseny, 2013)

(5 pont)

A beküldési határidő 2013. december 10-én LEJÁRT.

Megoldás. Első észrevételünk a következő.

1. lemma. Legyenek $\displaystyle A$ és $\displaystyle B$ egész számokból álló véges halmazok. Ekkor

$\displaystyle |A+B|\ge |A|+|B|-1.$

Bizonyítás. Jelölje $\displaystyle A$ elemeit $\displaystyle a_1<a_2<\dots<a_n$, valamint $\displaystyle B$ elemeit $\displaystyle b_1<b_2<\dots<b_m$. Ekkor

$\displaystyle a_1+b_1<a_2+b_1<a_2+b_2<\dots<a_{n-1}+b_m<a_n+b_m$

felsorol $\displaystyle n+m-1$ különböző elemet $\displaystyle A+B$-ben. (Mindegy, hogy a tagok indexeit hogyan növeljük.) $\displaystyle \blacksquare$

Hogyha maradékosztályokra bontunk modulo $\displaystyle q$, az alábbi erősítést kapjuk.

2. lemma. Amennyiben $\displaystyle A$ tartalmaz $\displaystyle r$-féle maradékot modulo $\displaystyle q$, teljesül, hogy

$\displaystyle |A+q\cdot B|\ge r|B|+(|A|-r).$

Bizonyítás. Jelölje $\displaystyle a_1,a_2,\dots,a_r$ a legkisebb értéket az egyes maradékosztályokban. Ekkor $\displaystyle A+q\cdot B$ tartalmazza $\displaystyle a_1+q\cdot B,a_2+q\cdot B,\dots,a_r+q\cdot B$ elemeit. Ez összesen $\displaystyle r|B|$ elem, hiszen különböző maradékosztályokba tartoznak.

Ezenfelül, ha az $\displaystyle a_i$ mod $\displaystyle q$ maradékosztályban szereplő elemek $\displaystyle a_i=a_{i,1}<a_{i,2}<\dots<a_{i,k}$, és $\displaystyle \max B=b_{max}$, akkor

$\displaystyle \max(a_i+q\cdot B)=a_i+qb_{max}<a_{i,2}+qb_{max}<\dots<a_{i,k}+qb_{max}$

további $\displaystyle k-1$ elemét adja $\displaystyle A+q\cdot B$-nek, mely az $\displaystyle a_i$ mod $\displaystyle q$ maradékosztályba tartozik. Összesítve, ez $\displaystyle (|A|-r)$-rel javít a becslésen. $\displaystyle \blacksquare$

Térjünk rá a feladatra, rekurzív megközelítéssel.

1. észrevétel. Ha kiveszünk $\displaystyle A$-ból egy maradékosztályt, tehát az $\displaystyle (i+q\mathbb{Z})\cap A=A_i$ halmaz elemeit, akkor a maradékokat megkülönböztetve

$\displaystyle |A+q\cdot A|\ge |A_i+q\cdot A|+|(A\setminus A_i)+q\cdot (A\setminus A_i)|.$

Itt az 1. lemma szerint fennáll, hogy $\displaystyle |A_i+q\cdot A|\ge |A_i|+|q\cdot A|-1=|A_i|+|A|-1$.

2. észrevétel. Maradékosztályokra bontva,

$\displaystyle |A+q\cdot A|\ge \sum_{i=0}^{q-1} |A_i+q\cdot A|\ge \sum_{i=0}^{q-1} |A_i+q\cdot A_i|.$

Legyen $\displaystyle A_i=i+q\cdot B_i$, ekkor $\displaystyle |A_i+q\cdot A_i|=|B_i+q\cdot B_i|$. Amennyiben $\displaystyle B_i$-ben minden mod $\displaystyle q$ maradék előfordul, $\displaystyle |B_i+q\cdot B_i|\ge (q+1)|B_i|-q$ (2. lemma). Tehát amennyiben minden $\displaystyle B_i$ vagy üres, vagy tartalmaz minden mod $\displaystyle q$ maradékot:

$\displaystyle |A+q\cdot A|\ge \sum_{B_i\neq \emptyset} (q+1)|B_i|-q\ge (q+1)|A|-q^2.$

3. észrevétel. Erősíthető az 1. észrevétel, ha szemügyre vesszük $\displaystyle A_i+q\cdot A$ azon elemeit, melyeket $\displaystyle A_i+q\cdot A_i$ nem tartalmaz. Tekintsük az $\displaystyle a+q\cdot A^*$ halmazt, ahol $\displaystyle a\in A_i$ és $\displaystyle A^*\subset A\setminus A_i$. Ha ez valamely $\displaystyle a\in A_i$-re diszjunkt $\displaystyle A_i+q\cdot A_i$-től, akkor

$\displaystyle |A_i+q\cdot A|\ge |A_i+q\cdot A_i|+|A^*|.$

Egyéb esetben minden $\displaystyle a\in A_i$-hez létezik $\displaystyle a^*\in A^*$ és $\displaystyle a',a''\in A_i$, melyre $\displaystyle a+qa^*=a'+qa''$. Vagyis minden $\displaystyle b\in B_i$-hez létezik $\displaystyle b'\in B_i$, melyre $\displaystyle b+a^*=b'+a''$.

Alkalmazzuk ezt $\displaystyle A^*=A_j=(j+q\mathbb{Z})\cap A$ választással valamely $\displaystyle j\neq i$-re. Tehát

$\displaystyle |A_i+q\cdot A|\ge |A_i+q\cdot A_i|+\min_{j\neq i}|A_j|,$

egyébiránt minden $\displaystyle b\in B_i$-hez létezik $\displaystyle b'\in B_i$, melyre $\displaystyle b'\equiv b+(j-i)\pmod q$. Hogyha a lehetséges $\displaystyle (j-i)$ értékek legnagyobb közös osztója $\displaystyle 1$, kapjuk, hogy $\displaystyle B_i$-ben minden mod $\displaystyle q$ maradék előfordul, és a 2. észrevétel alkalmazható. Ha pedig $\displaystyle d>1$ közös osztó, akkor nézhetjük $\displaystyle A$ helyett a kisebb átmérőjű $\displaystyle (A-i)/d\subset \mathbb{Z}$ halmazt.

Eredmény. Legyen $\displaystyle f(n)=\min\{|A+q\cdot A|:|A|=n\}$, és jelölje $\displaystyle m$ a legkisebb nem üres $\displaystyle A_i$ nagyságát. Ekkor vagy $\displaystyle f(n)\ge (q+1)n-q^2$, vagy pedig

$\displaystyle f(n)\ge \max \{ m+n-1+f(n-m),m+f(m)+f(n-m)\}.$

Következmény. $\displaystyle f(n)\ge \max \left\{\frac{\mu}{q+1}n-q^22^{\mu-3(q+1)}|\mu=3(q+1),3(q+1)+1,\dots,(q+1)^2\right\}$ (lásd a hivatalos megoldást).

Statisztika:

2 dolgozat érkezett.
0 pontot kapott:	2 versenyző.

A KöMaL 2013. novemberi matematika feladatai