 |
Az A. 864. feladat (2023. november) |
A. 864. Legyen ABC egy tetszőleges háromszög, O pedig a körülírt körének a középpontja. Legyen D, E, illetve F az ABC háromszög beírt körének érintési pontja a BC, a CA, illetve az AB oldalon. Legyen M, illetve N az AB, illetve az AC oldal felezőpontja. Legyen M′, illetve N′ az M, illetve az N tükörképe a DE, illetve a DF egyenesre. A CM′, illetve a BN′ egyenes a DE, illetve a DF egyenest messe a H, illetve a J pontban.
Bizonyítandó, hogy H, J és O egy egyenesre esik.
Javasolta: Luu Dong (Vietnám)
(7 pont)
A beküldési határidő 2023. december 11-én LEJÁRT.
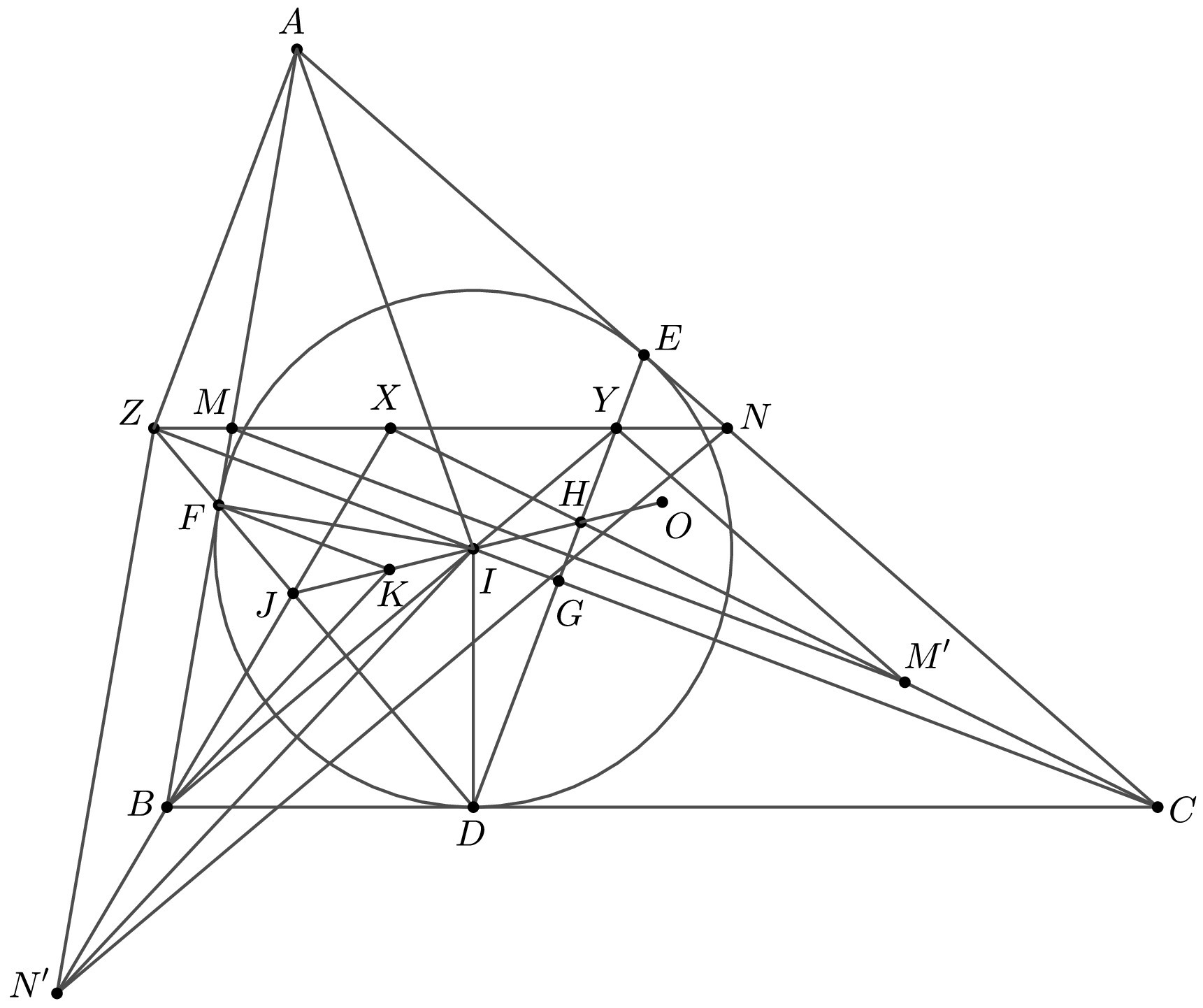
Legyen I az ABC háromszög beírt körének középpontja. Legyen X az MN és CH egyenesek metszéspontja. Legyen Y a BI és DE egyenesek metszéspontja. Legyen Z a CI és DF egyenesek metszéspontja. Jelölje K a DEF háromszög magasságpontját. Végül legyen G az DE szakasz felezőpontja. Az ABC háromszög szögeit a szokásos α, β, γ-val jelöljük.
Három ismert lemmával és a bizonyításaik vázlatával kezdjük a megoldást.
1. Lemma: A Z pont az MN egyenesre esik és AZC∢=90∘.
Bizonyítás vázlat: Szögszámolásból α2=FZI∢=FAI∢, tehát A,Z,F,I egy körön vannak. Ez azt jelenti, hogy AZC∢=AFI∢=90∘. Így N az AZC kör középpontja, tehát CZN∢=NCZ∢=ZCB∢, tehát ZN∥BC, ami azt jelenti, hogy M a ZN egyenesen van.
2. Lemma: K, I és O egy egyenesen vannak.
Bizonyítás vázlat: Legyenek A′, B′, C′ az ABC háromszög hozzáírt köreinek középpontjai. A A′B′C′ háromszög oldalai párhuzamosak a DEF háromszög oldalaival, tehát létezik egy középpontos hasonlóság (negatív aránnyal), amely A′B′C′-t DEF-be viszi. Ez azt jelenti, hogy a két háromszög Euler-egyenese párhuzamos. Vegyük észre, hogy I a DEF háromszög köréírt körének középpontja, és K a magasságpontja, tehát IK a DEF háromszög Euler-egyenese. Továbbá I az A′B′C′ háromszög magasságpontja és O Feuerbach-körének középpontja, tehát IO az A′B′C′ Euler-egyenese. Ebből következik a lemma állítása.
3. Lemma: 2⋅IG=FK
Bizonyítás vázlat: Tudjuk, hogy K a DEF háromszög magasságpontja, és I a köréírt körének középpontja. Szögszámolásból K′, K tükörképe G-re, a DEF körön van, továbbá ez a pont az F-el átellenes pont ezen a körön. Így IG az FKK′ háromszög középvonala, ami igazolja a lemmát.
Logikai szimmetriából Y is az MN egyenesre esik, mint X az 1. Lemma alapján. Mivel CE=CD, ezért EN=YN, tehát
DYM′∢=DYM∢=NYE∢=YEN∢.
Ez azt jelenti, hogy YM′∥EC. Hasonlóan ZN′∥FB. Könnyen látható, hogy MM′∥CZ, tehát
YXYN=M′XM′C=MXMZ.
Vegyük észre, hogy ha X′ az N′B és MN metszéspontja, akkor hasonlóan látható, hogy
YX′YN=MX′MZ,
ami azt jelenti, hogy X=X′, tehát N′, B és X egy egyenesen vannak. A Papposz-tételt alkalmazva a Z,X,Y,B,D és C pontokra kapjuk, hogy BX∩DZ=J, CX∩DY=H, BY∩CZ=I egy egyenesen vannak.
Szögszámolásból AIZ∢=FIB∢=90∘−β2. Ezt összevetve az 1. Lemmával, az AZI és BFI háromszögek hasonlóak, tehát ZI⋅BF=AZ⋅IF. A 1. Lemmát ismét felhasználva AZ=AC⋅sinγ2. Világos, hogy IDG∢=γ2. A 3. Lemma és az 1. Lemma felhasználásával
AZ⋅IF=AC⋅sinγ2⋅ID=2ZN⋅sin(IDG∢)⋅ID=2ZN′⋅IG=ZN′⋅FK.
Ebből következik, hogy ZI⋅BF=ZN′⋅FK. Tehát
FKZI=BFZN′=JFJZ.
Ez azt jelenti, hogy a J,K és I pontok egy egyenesen vannak. Korábban bizonyítottuk, hogy J,H és I egy egyenesen vannak, és a 2. Lemma szerint K,I és O is egy egyenesen vannak. Ezeket összevetve J,K,I,H és O mind egy egyenesen vannak, ami befejezi a bizonyítást.
Statisztika:
15 dolgozat érkezett. 7 pontot kapott: Bodor Mátyás, Czanik Pál, Diaconescu Tashi, Philip Stefanov, Simon László Bence, Tianyue DAI, Varga Boldizsár, Virág Rudolf, Wiener Anna. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2023. novemberi matematika feladatai
|
|

