 |
Az A. 871. feladat (2024. január) |
A. 871. Az ABC tompaszögű háromszögnek H a magasságpontja. Jelölje ωA az A középpontú, AH sugarú kört, ωB és ωC hasonlóan vannak definiálva. Az ABC háromszög síkjának minden X pontjára definiáljuk az Ω(X) kört a következőképpen (ha értelmezhető): vegyük X polárisait az ωA, ωB és ωC körökre nézve, és legyen Ω(X) a három egyenes által alkotott háromszög körülírt köre.
Keressük meg (esetleg véges sok kivétellel) azoknak az X pontoknak a halmazát a síkon, amelyekre X rajta van Ω(X)-en.
Javasolta: Molnár-Szabó Vilmos (Budapest)
(7 pont)
A beküldési határidő 2024. február 12-én LEJÁRT.
Jelölje XA, XB és XC az X pont inverz képét az ωA, ωB és ωC körökre, és legyen A′, B′ és C′ a H magasságpont tükörképe a BC, CA és AB oldalakra (jól ismert, hogy ezek a körülírt körön vannak). Könnyen megállapítható, hogy pl. A′ rajta van ωB-n és ωC-n is, hiszen az egyik metszéspontjuk H, a centrálisuk pedig BC. Most bebizonyítjuk, hogy az XXAXB háromszög körülírt köre a HC′ Apollóniusz köre.

Felhasználjuk azt az ismert állítást, hogy az inverzió alapköre egy pont és inverz képének az apollóniusz-köre. Ezek alapján ωA az XXA szakasz apollóniusz köre, ωB az XXB apollóniusz köre. A kettő metszéspontja H és C′, így HX/HXA=C′X/C′XA és HX/HXB=C′X/C′XB. Átrendezve ezeket kapjuk, hogy HX/C′X=HXA/C′XA=HXB/C′XB, azaz X, XA és XB rajta van HC′ apollóniusz körén, ahogy állítottuk. Jelölje az XXAXB háromszög körülírt körének a középpontját OC, OA és OB hasonlóan van definiálva.
Most tekintsünk egy olyan H középpontú inverziót, amely A-t A′-be, B-t B′-be és C-t C′-be viszi. Absztrakt értelemben mindig van ilyen inverzió (képzetes sugarú körrel), de hagyományos értelemben éppen akkor van, ha H kívül van ABC körülírt körén, azaz a háromszög tomapszögű. Ebben az esetben jelölje k az inverzió alapkörét, és X képe ennél az inverziónál legyen X′.
A feladatra térve ismert állítás, hogy X polárisa ωA -ra nézve az XH-ra állított merőleges az XA pontban. Hasonló a helyzet ωB esetén is, azaz a két poláris metszéspontja éppen az XXAXB körülírt körének az X ponttal szemközti pontja (a Thálész-tétel alapján). Ha az X pontból a felére kicsinyítjük az ábrát, akkor a feladat feltétele átalakul azzá, hogy X, OA, OB és OC egy körre esnek. Írányított szögekel modulo 180∘ számolva azt kapjuk, hogy a feltétel ekivivalens azzal, hogy OCXOB∢=OCOAOB∢. Próbáljunk meg valamit kezdeni ezekkel a szögekkel.
Vegyük észre, hogy OAOC merőleges XB-re: az XXBXC és XXAXB egymást X-ben és XB-ben metszi, azaz XXB merőleges a két kör centrálisára, de X, XB és B egy egyenesre esnek, hiszen XB az X inverz képe a B középpontú ωB körre nézve. Hasonlóan OAOB és XC is merőleges, azaz OCOAOB∢=BXC∢ (továbbra is előjelesen, modulo 180∘ számolva).
Most vizsgáljuk meg az OCXOB∢ szöget. OCXOB∢=HXOB∢−HXOC∢. A HXOB∢ szög vizsgálatánál arra támaszkodunk, hogy korábban láttuk, hogy az XXAXC kör a HB′ Apollóniusz-köre, melynek középpontja OB, és így jól ismert (és az ábrán könnyen ellenőrizhető) módon HXOB∢=OBB′X∢=HB′X∢.
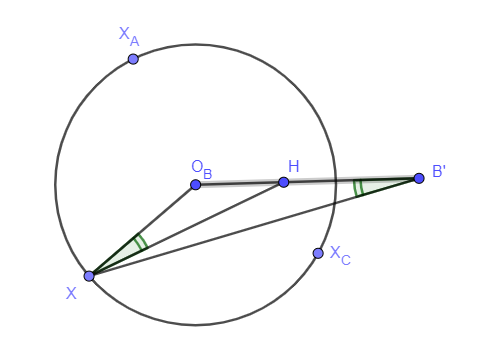
Végül H középponttal invertálva a k körre adódik, hogy HB′X∢=−HX′B∢, hiszen B és B′ egymás inverz képe erre a körre. Így végül OCXOB∢=HXOB∢−HXOC∢=HB′X∢−HC′X∢==HX′C∢−HX′B∢=BX′C∢.
Az előző két bekezdést összevetve tehát BXC∢=BX′C∢, ami pontosan akkor teljesül, ha B, C, X és X′ egy körre esnek. Ez pontosan akkor teljesül, ha X=X′, azaz X rajta van a k körön, egyébként pedig, mivel az X és X′ ponton átmenő körök merőlegesek k-ra (az inverzió invariáns körei), és a B és C ponton átmenő fix kör éppen az ABC háromszög körülírt köre, ezért pontosan akkor, ha X rajta van ezen a körön.
Azaz a feladat kérdésére a válasz: az ABC háromszög körülírt köre és a H középpontú, erre merőleges kör. Megjegyezzük, hogy ez a válasz hegyesszögű háromszögre is helyes, csak az utóbbi kör nem létezik, azaz ilyenkor csak az ABC háromszög körülírt köre elégíti ki a feladat feltételeit.
Megjegyzés: a k körre való invertálásnál az ωA kör képe éppen a BC egyenes lesz, így az ωA-ra való invertálásból BC-re való tükrözés lesz. A Simson-tétel miatt a feladat feltétele ekvivalens azzal, hogy XA, XB és XC egy egyenesre esnek, azaz az invertálás után ebből az lesz, hogy X′ tükörképei az ABC háromszög oldalegyeneseire és a H pont egy körre vagy egyenesre esnek. Jól ismert, hogy a körülírt kör pontjainak tükörképei egy H-n átmenő egyenesre esnek, így ebből adódik, hogy ha X′ rajta van a körülírt körön, akkor kielégíti a feladat feltételeit, de mivel a körülírt kör a k-ra való inverzió invariáns köre, ezért ez pontosan akkor igaz, ha X rajta van a körülírt körön: ezzel a válasz könnyebbik felét megkaptuk.
Statisztika:
7 dolgozat érkezett. 7 pontot kapott: Bodor Mátyás, Varga Boldizsár, Wiener Anna. 6 pontot kapott: Foris Dávid. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző.
A KöMaL 2024. januári matematika feladatai
|
|

