Problem A. 878. (April 2024)

A. 878. Let point \(\displaystyle A\) be one of the intersections of circles \(\displaystyle c\) and \(\displaystyle k\). Let \(\displaystyle X_1\) and \(\displaystyle X_2\) be arbitrary points on circle \(\displaystyle c\). Let \(\displaystyle Y_i\) denote the intersection of line \(\displaystyle AX_i\) and circle \(\displaystyle k\) for \(\displaystyle i=1,2\). Let \(\displaystyle P_1\), \(\displaystyle P_2\) and \(\displaystyle P_3\) be arbitrary points on circle \(\displaystyle k\), and let \(\displaystyle O\) denote the center of circle \(\displaystyle k\). Let \(\displaystyle K_{ij}\) denote the center of circle \(\displaystyle (X_iY_iP_j)\) for \(\displaystyle i=1,2\) and \(\displaystyle j=1,2,3\). Let \(\displaystyle L_j\) denote the center of circle \(\displaystyle (OK_{1j}K_{2j})\) for \(\displaystyle j=1,2,3\). Prove that points \(\displaystyle L_1\), \(\displaystyle L_2\) and \(\displaystyle L_3\) are collinear.

Proposed by Vilmos Molnár-Szabó, Budapest

(7 pont)

Deadline expired on May 10, 2024.

The basis of the proof is the following less well know rephrasing of the inscribed angle theorem: if we fix two points in the plane, and rotate lines around them with the same (oriented) angular speed, the intersections of the two rotating lines will be on a circle containing the two fixed points.

Now we prove the following statement which will also lead to the solution of the original problem:

Claim: Let point \(\displaystyle X\) be on circle \(\displaystyle c\) and point \(\displaystyle Y\) be on circle \(\displaystyle k\) such that \(\displaystyle X\), \(\displaystyle Y\) and one of the intersections of the two circles, point \(\displaystyle A\) are collinear. Let \(\displaystyle P\) be an arbitrary point on circle \(\displaystyle k\). Now if we move point \(\displaystyle X\) on \(\displaystyle c\) (\(\displaystyle P\) stays fixed), the center of circle \(\displaystyle PXY\) will move on a circle containing point \(\displaystyle O\) (the center of circle \(\displaystyle k\)).

Proof: The key insight is this: if we move \(\displaystyle X\) around circle \(\displaystyle c\) with constant angular speed, point \(\displaystyle Y\) will move on circle \(\displaystyle k\) with the same (oriented) angular speed (this is an easy consequence of the inscribed angle theorem). This means that lines \(\displaystyle XY\) and \(\displaystyle YP\) also rotate with the same constant angular speed, so the same is also true for their perpendicular bisectors. If we find fixed points for both of them, we are done based on our initial remark. In the case of the perpendicular bisector of \(\displaystyle PY\) this is easy: it passes through the center of circle \(\displaystyle k\), i.e. point \(\displaystyle O\).

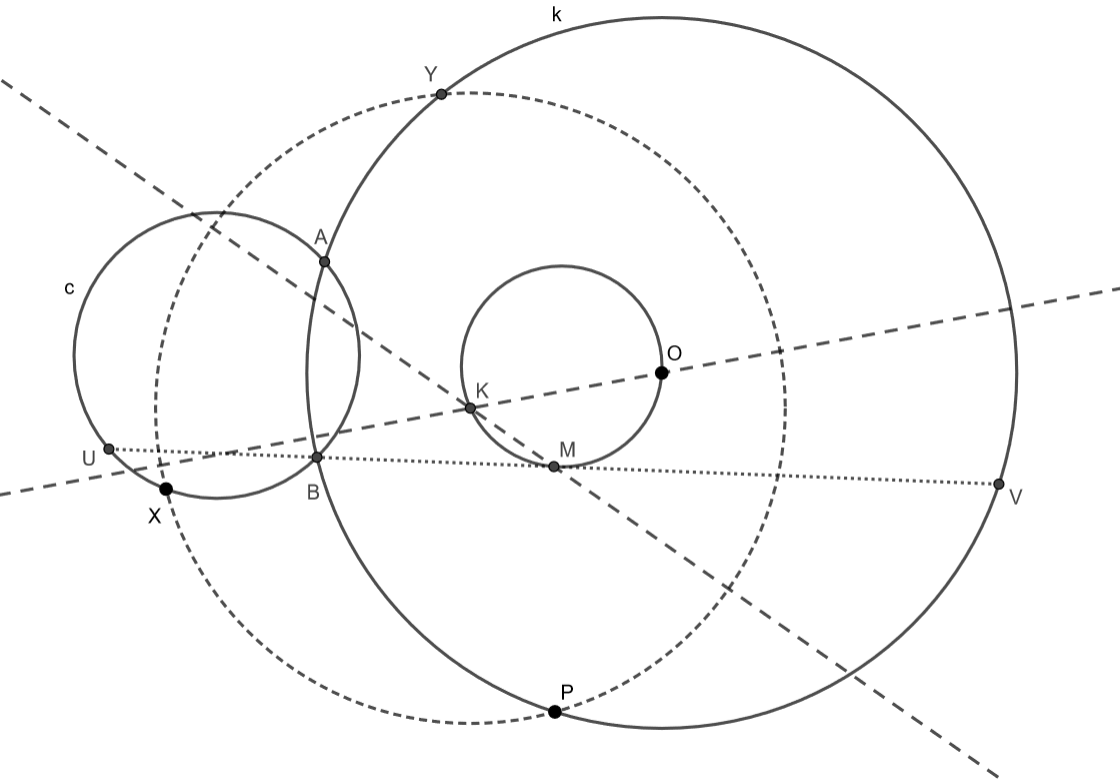
In the case of line segment \(\displaystyle XY\) it's a bit more challenging to find the common point: we claim that it always passes through point \(\displaystyle M\), which is defined in the following way: draw a parallel with the common axis of symmetry of the two circles though the other common point of the two given circles (point \(\displaystyle B\)), and take its intersections \(\displaystyle U\) and \(\displaystyle V\) with the two given circles. Let \(\displaystyle M\) be the midpoint of line segment \(\displaystyle UV\).

Indeed, we have to show that \(\displaystyle MX=MY\). Note that quadrilateral \(\displaystyle UXYV\) is a right trapezoid (with the right angles at \(\displaystyle X\) and \(\displaystyle Y\)) based on Thales's theorem (it can be self intersecting, too, but that does not affect the next argument). Now if we reflect \(\displaystyle X\) and \(\displaystyle Y\) across \(\displaystyle M\), we get rectangle \(\displaystyle XYX'Y'\). Therefore, diagonals \(\displaystyle XX'\) and \(\displaystyle YY'\) has the same length, and thus also their halves must have the same length, and we are done.

Now the statement of the problem became obvious: since points \(\displaystyle M\) and \(\displaystyle O\) are independent from the choice of \(\displaystyle P\), the center of the circle containing \(\displaystyle K\) will always be on the perpendicular bisector of \(\displaystyle OM\), and thus our proof is concluded.

Remark: in the argument the idea of the moving points and rotating lines can be substituted with the following simple argument: angles \(\displaystyle \angle MKO\) and \(\displaystyle \angle XYP\) are equal, since their rays are perpendicular to each other, and it's easy to see (by applying the inscribed angle theorem) that the latter does not depend on the choice of \(\displaystyle X\) and \(\displaystyle Y\).

Statistics:

8 students sent a solution.
7 points:	Bodor Mátyás, Czanik Pál, Diaconescu Tashi, Forrai Boldizsár, Philip Stefanov, Szakács Ábel, Varga Boldizsár, Wiener Anna.

Problems in Mathematics of KöMaL, April 2024