Az A. 878. feladat (2024. április)

A. 878. Legyen $\displaystyle A$ a $\displaystyle c$ és $\displaystyle k$ körök egyik metszéspontja. Legyen $\displaystyle X_1$ és $\displaystyle X_2$ tetszőleges pont a $\displaystyle c$ körön. Jelölje $\displaystyle Y_i$ az $\displaystyle AX_i$ egyenes második metszéspontját a $\displaystyle k$ körrel $\displaystyle i=1,2$ esetén. Legyen $\displaystyle P_1$, $\displaystyle P_2$ és $\displaystyle P_3$ tetszőleges pont a $\displaystyle k$ körön, és jelölje $\displaystyle O$ a $\displaystyle k$ kör középpontját.

Jelölje $\displaystyle K_{ij}$ az $\displaystyle X_iY_iP_j$ háromszög körülírt körének középpontját $\displaystyle i=1$, $\displaystyle 2$ és $\displaystyle {j=1}$, $\displaystyle 2$, $\displaystyle 3$ esetén. Legyen $\displaystyle L_j$ az $\displaystyle OK_{1j}K_{2j}$ háromszög körülírt körének középpontja $\displaystyle j=1$, $\displaystyle 2$, $\displaystyle 3$ esetén. Bizonyítsuk be, hogy $\displaystyle L_1$, $\displaystyle L_2$ és $\displaystyle L_3$ egy egyenesre esik.

Javasolta: Molnár-Szabó Vilmos (Budapest)

(7 pont)

A beküldési határidő 2024. május 10-én LEJÁRT.

A feladat megoldásának alapgondolata a következő állítás, amely a kerületi szögek tételének egy kevésbé ismert átfogalmazása: ha két adott pont körül ugyanakkora szögsebességgel ugyanabban az irányban forgatunk egy-egy egyenest, akkor a két forgó egyenes metszéspontjai egy kört fognak leírni, mely átmegy a két rögzített ponton.

Állítás: Legyen $\displaystyle X$ a $\displaystyle c$ körön, $\displaystyle Y$ az $\displaystyle O$ középpontú $\displaystyle k$ körön úgy, hogy $\displaystyle X$, $\displaystyle Y$ és a két kör metszéspontja, az $\displaystyle A$ pont egy egyenesre essen. Legyen $\displaystyle P$ a $\displaystyle k$ kör tetszőleges pontja. Ekkor az $\displaystyle X$ pontot a $\displaystyle c$ körön mozgatva (a $\displaystyle P$ pontot fixen tartva) a $\displaystyle PXY$ kör $\displaystyle K$ középpontja egy $\displaystyle O$-n átmenő körön fog mozogni.

Bizonyítás: Vegyük észre a következőt: ha az $\displaystyle X$ pontot egyenletes szögsebességgel mozgatom a $\displaystyle c$ körön, $\displaystyle Y$ is egyenletes szögsebességgel mozog a $\displaystyle k$ körön ugyanolyan irányban (ez a kerületi szögek tételének egyszerű következménye). Ilyenkor az $\displaystyle XY$ és az $\displaystyle YP$ egyenes is egyenletes szögsebességgel forog körbe ugyanolyan irányban, és ez azt jelenti, hogy a felezőmerőlegeseik is egyenletes szögsebességgel forognak körbe ugyanolyan irányban. Ha megmutatjuk, hogy van fixpontjuk, akkor a kerületi szögek tételének megfordítása alapján a metszéspontjaik egy körre fognak esni. A $\displaystyle PY$ felezőmerőlegese esetén ez egyszerű, mert mind átmennek az $\displaystyle O$ ponton (az ábrán a szaggatott egyenesek a vizsgált felezőmerőlegesek).

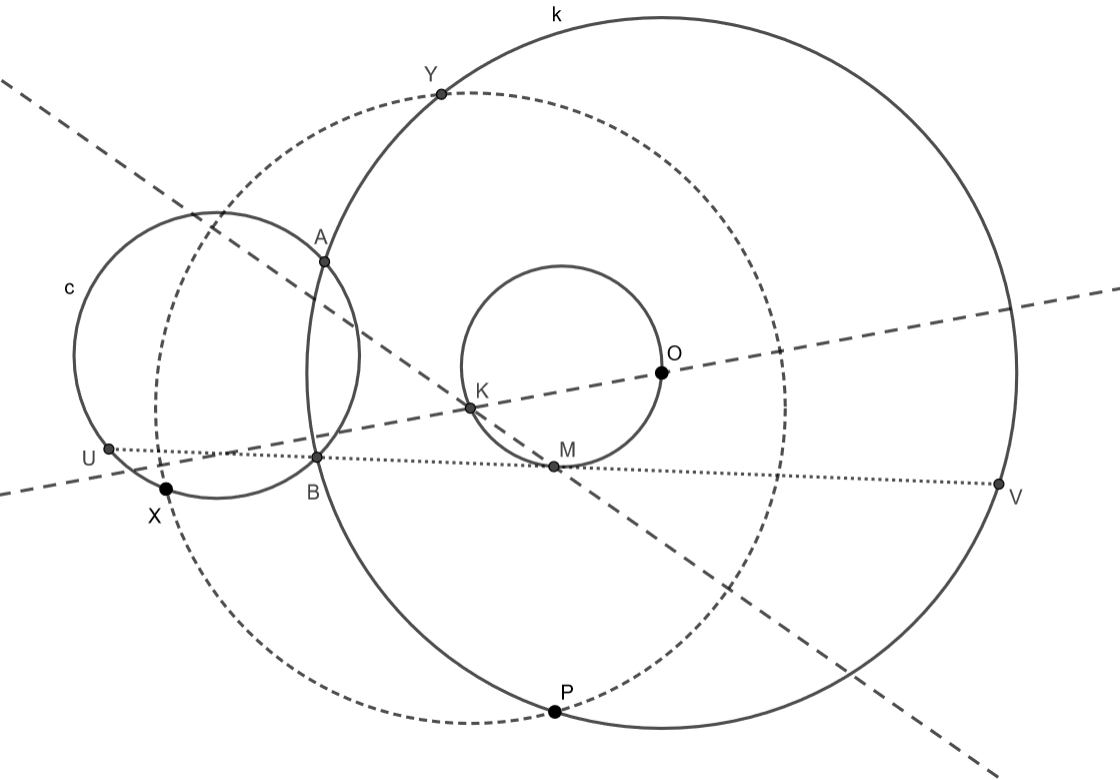
Az $\displaystyle XY$ szakasz felezőmerőlegese esetén kicsit trükkösebb megtalálni ezt a pontot: az $\displaystyle M$ pontot úgy kaphatjuk meg, hogy vesszük a két kör másik metszéspontján, a $\displaystyle B$ ponton áthaladó, a két kör közös szimmetritengelyével párhuzamos egyenes metszéspontjait a két körrel, $\displaystyle U$-t és $\displaystyle V$-t, $\displaystyle M$ pedig az így kapott szakasz felezőpontja lesz.

Ennek belátásához vegyük észre, hogy $\displaystyle XU$ és $\displaystyle YV$ is merőleges $\displaystyle XY$-ra A Thálesz-tétel és a megfordítása miatt (hiszen $\displaystyle ABU\sphericalangle = ABV\sphericalangle = 90^{\circ}$, azaz $\displaystyle AU$ és $\displaystyle AV$ átmérő a megfelelő körben). Mivel $\displaystyle M$ felezi $\displaystyle UV$-t, egyforma messze van az $\displaystyle XU$ és az $\displaystyle YV$ egyenestől is, de mivel $\displaystyle XY$ merőleges a két egyenesre, így $\displaystyle M$ rajta van $\displaystyle XY$ felezőmerőlegesén, amely egyben az $\displaystyle XU$ és $\displaystyle YV$ egyenesektől egyforma távol lévő pontok halmaza is.

Innen pedig már a feladat állítása magától értetődő: mivel sem az $\displaystyle O$, sem az $\displaystyle M$ pont nem függ a $\displaystyle P$ pont választásától, a kapott körök középpontja mindig rajta van az $\displaystyle OM$ felezőmerőlegesén, készen vagyunk.

Megjegyzés: a megoldásban a mozgó pontok és forgó egyenesek gondolata helyettesíthető a következő egyszerű megfontolással is: merőleges szárú szögek miatt $\displaystyle MKO\sphericalangle=XYP\sphericalangle$, ez utóbbiról pedig nem nehéz látni a kerületi szögek tételével, hogy nem függ az $\displaystyle X$ és $\displaystyle Y$ választásától.

Statisztika:

8 dolgozat érkezett.
7 pontot kapott:	Bodor Mátyás, Czanik Pál, Diaconescu Tashi, Forrai Boldizsár, Philip Stefanov, Szakács Ábel, Varga Boldizsár, Wiener Anna.

A KöMaL 2024. áprilisi matematika feladatai