 |
Az A. 885. feladat (2024. szeptember) |
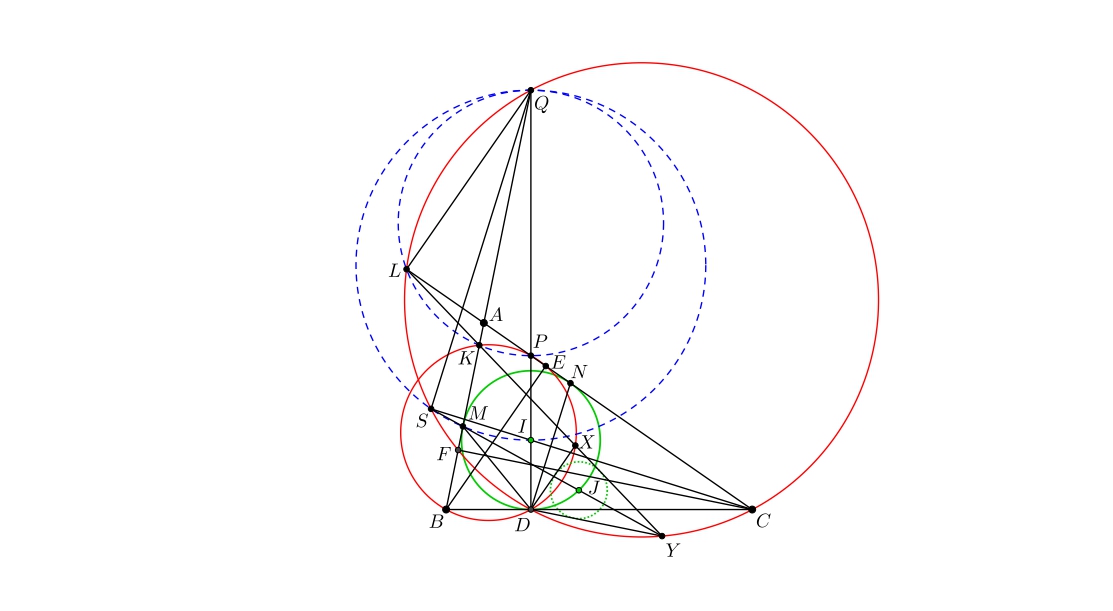
A. 885. Legyen adva egy hegyesszögű nem egyenlőszárú \(\displaystyle ABC\) háromszög. Legyen \(\displaystyle BE\) és \(\displaystyle CF\) a háromszög két magassága, \(\displaystyle D\) pedig jelölje a háromszög beírt körének érintési pontját a \(\displaystyle BC\) oldalon. A \(\displaystyle BDE\) háromszög körülírt köre messe az \(\displaystyle AB\) egyenest másodszor a \(\displaystyle K\) pontban, a \(\displaystyle CDF\) háromszög körülírt köre messe az \(\displaystyle AC\) egyenest másodszor az \(\displaystyle L\) pontban. A \(\displaystyle BDE\) és a \(\displaystyle CDF\) háromszögek körülírt körei a \(\displaystyle KL\) egyenest másodszor rendre az \(\displaystyle X\) és az \(\displaystyle Y\) pontban metszik. Bizonyítandó, hogy a \(\displaystyle DXY\) háromszög beírt körének középpontja az \(\displaystyle ABC\) háromszög beírt körére esik.
Javasolta: Luu Dong, Vietnam
(7 pont)
A beküldési határidő 2024. október 10-én LEJÁRT.
Legyen \(\displaystyle k\) az \(\displaystyle ABC\) háromszög beírt köre, \(\displaystyle I\) a középpontja. Jelölje a \(\displaystyle DI\) egyenes és az \(\displaystyle AC, AB\) egyenesek metszéspontját rendre \(\displaystyle P, Q\). Jelölje \(\displaystyle M, N\) a \(\displaystyle k\) kör érintési pontjait az \(\displaystyle AB\) és \(\displaystyle AC\) oldalakon. A \(\displaystyle CI\) másodszor messe \(\displaystyle S\)-ben \(\displaystyle CDF\) háromszög köréírt körét. Jelölje \(\displaystyle J\) a \(\displaystyle DXY\) háromszög beírt körének középpontját.
Világos, hogy a \(\displaystyle P, Q, K, L\) pontok egy körön fekszenek, amelynek átmérője \(\displaystyle PQ\). Ebből következik, hogy
\(\displaystyle (QF, QD)\angle= (QK, QP)\angle=(LK, LP)\angle=(LY, LC)\angle.\)
Tehát \(\displaystyle DY \parallel CF\). Hasonlóan, \(\displaystyle DX \parallel BE\).
Mivel \(\displaystyle CS\) az \(\displaystyle ACD \angle \) szögfelezője, ezért \(\displaystyle YS\) a \(\displaystyle KYD \angle\) szögfelezője. Ez azt jelenti, hogy \(\displaystyle S, J, Y\) kollineárisak. (1)
Tudjuk, hogy \(\displaystyle S, M, I, Q\) egy körön fekszenek, amelynek átmérője \(\displaystyle IQ\). Ez azt jelenti, hogy
\(\displaystyle (SM, SI)\angle=(QM, QI)\angle.\)
Ebből következik, hogy
\(\displaystyle (SM, SC)\angle =(QF, QD)\angle=(SY, SC)\angle.\)
Tehát \(\displaystyle S, M, Y\) kollineárisak. (2)
Az (1) és (2) állításokból következik, hogy \(\displaystyle M, J, Y\) kollineárisak. Hasonlóan, \(\displaystyle N, J, X\) is kollineárisak. Így a következőket kapjuk:
\(\displaystyle (XY, XD)\angle=(XH, XD)\angle=(BH, BD)\angle =-(BC, BA)\angle,\)
és hasonlóan,
\(\displaystyle (YX, YD)\angle=-(CB, CA)\angle.\)
Ebből következik, hogy a \(\displaystyle DXY\) és \(\displaystyle ABC\) háromszögek hasonlóak. Tehát a \(\displaystyle JXY\) és \(\displaystyle IBC\) háromszögek is hasonlóak. Végül
\(\displaystyle (JM, JN)\angle= (JY, JX)\angle=-(IC, IB)\angle=-(DN, DM)\angle=(DM, DN)\angle,\)
amiből következik, hogy \(\displaystyle J, M, N, D\) egy körön fekszenek.
Statisztika:
Az A. 885. feladat értékelése még nem fejeződött be.
A KöMaL 2024. szeptemberi matematika feladatai