 |
Az A. 891. feladat (2024. november) |
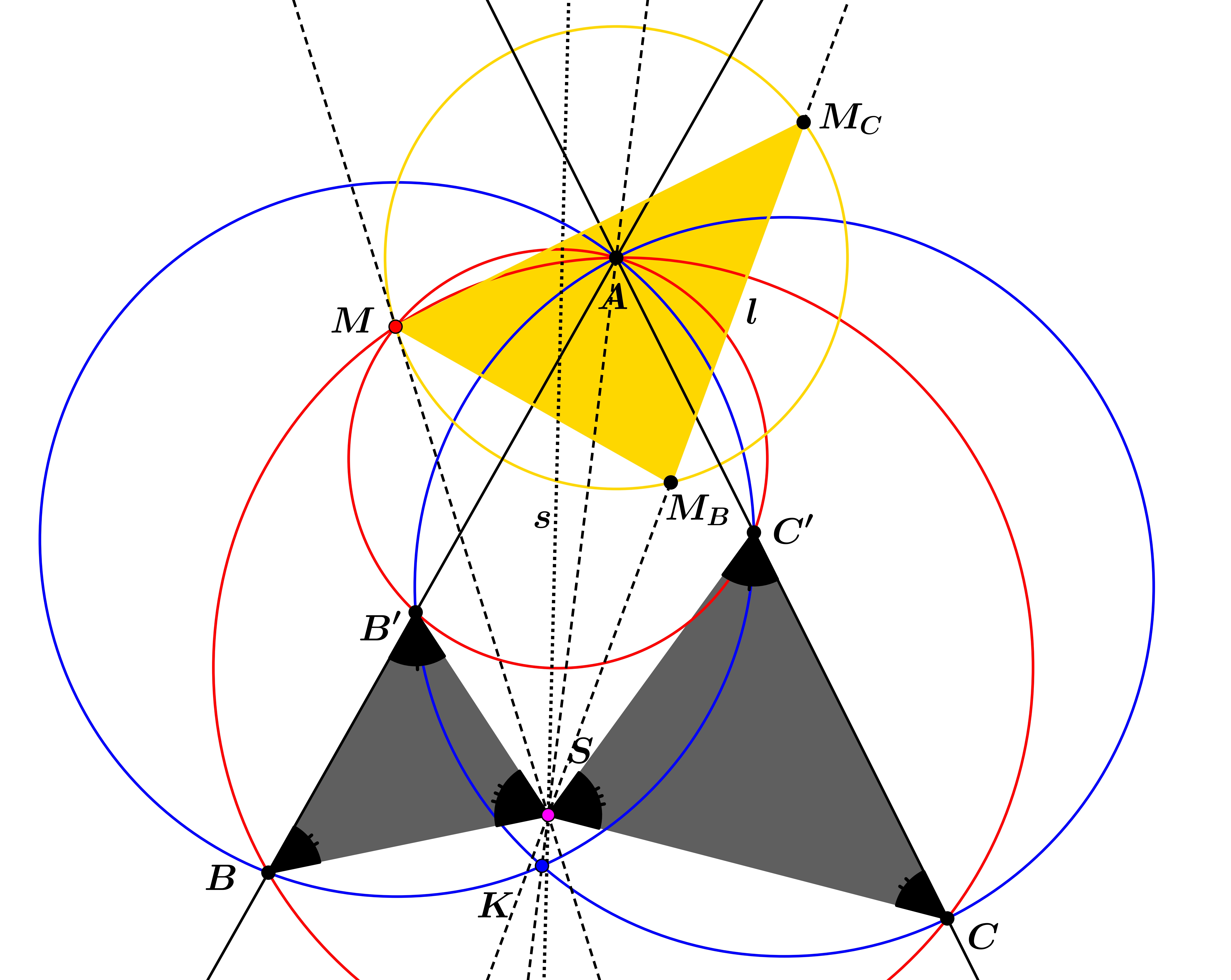
A. 891. Adott egy hegyesszögű ABC háromszög. A B′ és C′ pont rendre az AB és AC oldal belsejében helyezkedik el. Az ABC és AB′C′ háromszögek körülírt körei M-ben, az ABC′ és AB′C háromszögek körülírt körei pedig K-ban metszik egymást másodszor. Tükrözzük M-et az AB és AC egyenesre, a két tükörképen átmenő egyenest jelöljük l-lel.
a) Bizonyítsuk be, hogy az M-en átmenő, AM-re merőleges egyenes, az AK egyenes és l vagy egy ponton mennek át, vagy mind párhuzamosak.
b) Igazoljuk, hogy ha a három egyenes az S ponton megy át, akkor az SBC′ és SCB′ háromszögek területe egyenlő.
Javasolta: Bán-Szabó Áron (Budapest)
(7 pont)
A beküldési határidő 2024. december 10-én LEJÁRT.
Először a második állítást bizonyítjuk be.
Jelölje MB és MC M tükörképét az AB ill. AC egyenesre. Jelölje továbbá S az M-en keresztül húzott merőleges és az l=MBMC egyenes metszéspontját. A tükrözések miatt AM=AMB=AMC, tehát A az MMBMC körülírt körének középpontja. Az SM egyenes érinti ezt a kört, hiszen AM-re merőleges. Az érintő szárú kerületi szögek tétele alapján SMMB∢=SMCM∢, így az SMMB és SMCM háromszögek hasonlók (szögeik páronként megegyeznek). Mivel ellentétes körüljárásúak, található egy L irányításváltó hasonlósági transzformáció, amely egymásba viszi őket és az S pontot fixen tartja (például az MSMB∢ szögfelezőjére való tükrözés és egy S középpontú középpontos hasonlóság egymásutánja). Ez a hasonlósági transzformáció az MBM szakaszt az MMC szakaszba képezi.
Most tekintsük a BMBM és CMCM háromszögeket. Mindkettő egyenlőszárú, hiszen B és C rajta van az MBM ill. az MCM felezőmerőlegesén. Azonban A mindkettő felezőmerőlegesen rajta van, így a kerületi szögek tétele alapján (az ABCM húrnégyszögben) MBMB=2MBA∢=2MCA∢=MCMC∢, azaz a két tekintett háromszög hasonló. Mivel a L hasonlóság az MBM szakaszt az MMC szakaszba viszi, így a körüljárásokat is figyelembe véve B képe a C pont. Ugyanez a gondolatmenet az AB′C′ háromszögre alkalmazva azt mutatja, hogy B′ képe a C′ pont. Így tehát L a BB′ szakaszt a CC′ szakaszba képezi (mivel az MBB′ és MCC′ háromszögek körüljárása azonos). Mivel S fixpontja ennek a transzformációnak, így SCC′ és SBB′ hasonló és ellentétes körüljárású.
Ez azonnal bizonyítja a feladat második felét. A hasonlóság miatt C′SB∢=CSB′∢ és BS/B′S=CS/C′S. Így pedig
TBC′S=12⋅BS⋅C′S⋅sin(BSC′∢)=12⋅CS⋅BS′⋅sin(B′SC)=TCB′S.
Most még az kell megmutatnunk, hogy AK is átmegy az S ponton. Vegyük észre, hogy azon X pontok mértani helye, melyre d(X,AB)/d(X,AC)=BB′/CC′, két A-n átmenő egyenes uniója. Tudjuk, M és K is ilyen (hiszen MBB′△∼MCC′△ és KBB′△∼KC′C△), sőt a korábbiak miatt S is. Ebből világos, hogy ez a két egyenes az AM és az AK egyenes lesz, ezek valamelyikén rajta kell legyen S, de mivel S≠M és SM⊥AM, S∈AK.
Előfordulhat persze, hogy az egyenesek nem metszik egymást egy S pontban. Ekkor a hasonlósági transzformációnkban a nyújtás helyett egy eltolás szerepel (azaz most egy irányításváltó egybevágóság), tehát SBB′ és SC′C most egymás tükörképe lesz, és a bizonyítás ugyanúgy megy.
Megjegyezzük, hogy az L transzformációt tükrözve nyújtásnak nevezik, és belátható, hogy minden irányításváltó hasonlósági transzformáció tükrözve nyújtás.
Statisztika:
10 dolgozat érkezett. 7 pontot kapott: Bodor Mátyás, Czanik Pál, Keresztély Zsófia, Szakács Ábel, Varga Boldizsár. 6 pontot kapott: Forrai Boldizsár, Minh Hoang Tran. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2024. novemberi matematika feladatai
|
|

