Az A. 892. feladat (2024. november)

A. 892. Adott két egész szám, $\displaystyle k$ és $\displaystyle d$ úgy, hogy $\displaystyle d$ osztója a $\displaystyle k^3-2$ számnak. Mutassuk meg, hogy ekkor léteznek olyan $\displaystyle a$, $\displaystyle b$, $\displaystyle c$ egész számok, amelyekre

$\displaystyle d=a^3+2b^3+4c^3-6abc.$

Javasolta: Beke Csongor és Simon László Bence (Cambridge)

(7 pont)

A beküldési határidő 2024. december 10-én LEJÁRT.

Legyen $\displaystyle k$ egy egész szám amire $\displaystyle k^3\equiv 2\pmod{d}$. Ekkor felhasználva a jól ismert $\displaystyle x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)$ azonosságot:

Tehát ahhoz, hogy $\displaystyle d\mid a^3+2b^3+2c^3-6abc$ elég annyi, hogy $\displaystyle d\mid a+k b+k^2 c$. Legyen $\displaystyle S\subset \mathbb{Z}^3$ azon $\displaystyle (a,b,c)$ rendezett egész számhármasok halmaza, amelyre teljesül $\displaystyle k\mid a+k b+k^2 c$.

Elöszőr belátjuk, hogy $\displaystyle S$ egy 3 dimenziós rács, azaz létezik $\displaystyle 3$ nemnulla vektor, $\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3$ úgy hogy $\displaystyle S$ megegyezik az $\displaystyle \left\{\kappa \mathbf{u}_1+\lambda\mathbf{v}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu \in \mathbb{Z}\right\}$ halmazzal, és az $\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3$ vektorok által meghatározott paralelpipedon térfogata pontosan $\displaystyle d$.

Legyenek $\displaystyle \mathbf{u}_1,\mathbf{u}_2, \mathbf{u}_3\in S\setminus \{\mathbf{0}\}$ olyan nem egy síkban lévő vektorok, melyek minimalizálják a paralelpipedon térfogatát (ilyenek léteznek, hiszen bármely három $\displaystyle \mathbb{Z}^3$-beli vektor által meghatározott paralelepipedon térfogata egész szám). Egyszerű látni, hogy ha $\displaystyle \mathbf{u}, \mathbf{v}\in S$, akkor $\displaystyle \mathbf{u}\pm\mathbf{v}\in S$, ezért

$\displaystyle \left\{\kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu\in \mathbb{Z}\right\}\subset S.$

Tegyük fel, hogy létezik olyan $\displaystyle \mathbf{v}$ vektor $\displaystyle S$-ben, amely nem esik bele ebbe a halmazba. Tekintsük ekkor az $\displaystyle \mathbf{u}_1,\mathbf{u}_2, \mathbf{u}_3$ által meghatározott paralelepipedon eltoltját a $\displaystyle \kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3$ vektorral úgy, hogy az tartalmazza a $\displaystyle \mathbf{v}$-t. Ekkor $\displaystyle \mathbf{u}_3$-at lecserélve $\displaystyle \mathbf{v}-(\kappa\mathbf{u}_1+\lambda\mathbf{v}_2+\mu\mathbf{u}_3)$-ra egy kisebb térfogatú paralelpipedont kapunk, ami ellentmondás, azaz

$\displaystyle \left\{\kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu\in \mathbf{Z}\right\}= S.$

Most még azt kell belátni, hogy a paralelepipedon térfogata $\displaystyle d$. Ehhez először belátjuk, hogy $\displaystyle [0,d-1]^3\cap S$-nek $\displaystyle d^2$ eleme van. Ez azért igaz, mert ha $\displaystyle b,c\in [0,d-1]$, akkor pontosan 1 darab $\displaystyle a\in [0,k-1]$ létezik, amelyre $\displaystyle d\mid a+k b+k^2 c$. Legyen a paralelepipedon átmérője $\displaystyle D$, térfogata $\displaystyle T$. Most tekintsük általánosabban a $\displaystyle Q_n=[0,dn-1]^3$ kockát ($\displaystyle n\in \mathbb{Z}^+$). Az előző gondolatmenetünkhöz hasonlóan kijön, hogy pontosan $\displaystyle d^2\cdot n^3$ eleme esik $\displaystyle S$-nek $\displaystyle Q_n$-be. Viszont ha a lefedő paralelepipedonokat nézzük, legalább $\displaystyle (nd-2D)^3/T$ teljesen benne van $\displaystyle Q_n$-ben, viszont $\displaystyle (nd+2D)^3/T$ darabbal le lehet fedni $\displaystyle Q_n$-t. Ezért igaz, hogy $\displaystyle (nd-2D)^3 \leq k^2\cdot n^3 \cdot T\leq (nd+2D)^3$ bármely $\displaystyle n\in \mathbb{N}$-re, ezért $\displaystyle T=d$.

Azt akarjuk belátni, hogy van olyan $\displaystyle (0,0,0) \neq (a,b,c) \in S$, amelyre

$\displaystyle f(a,b,c) =\vert a^3+2b^3+4c^3-6abc \vert < 3d.$

Ha találunk ilyet, akkor kész vagyunk, mert ha $\displaystyle f(a,b,c)=-d$, akkor $\displaystyle f(-a,-b,-c)=d$, ha $\displaystyle f(a,b,c)=2d$, akkor $\displaystyle 2 \vert a$, és ekkor $\displaystyle f(b,c,a/2)=d$. Ha $\displaystyle f(a,b,c)=-2k$, akkor persze $\displaystyle f(-b,-c,-a/2)=d$. Végül pedig $\displaystyle f(a,b,c) \neq 0$, mert ellenkező esetben $\displaystyle f(b,c,a/2)$ értéke is 0 (és persze $\displaystyle a/2$ is egész), és ezt az eljárást a végtelenségig folytatnák, ami $\displaystyle (a,b,c) \neq (0,0,0)$ esetén lehetetlen.

Ehhez a Minkowski-tételt hívjuk segítségül, ami azt mondja ki ebben az esetben, hogyha van egy origóra középpontosan szimmetrikus, konvex testünk, melynek legalább $\displaystyle 8d$ a térfogata, akkor van benne rácspont az origón kívül is. Tehát ha találunk egy elég nagy térfogatú, konvex, az origóra szimmetrikus testet, amelyben minden pontra $\displaystyle |f(x,y,z)| < 3d$, akkor kész vagyunk. Szimmetrizálni szeretnénk a képletet, ezért végzünk egy $\displaystyle 2^{-\frac{1}{3}}$-os affinitást az $\displaystyle x=0$ síkra, majd egy $\displaystyle 2^{\frac{1}{3}}$-os affinitást az $\displaystyle z=0$ síkra. Az arányok szorzata 1, ezért ez a transzformáció térfogattartó, és

$\displaystyle f(x,y,z)=2x'^3+2y^3+2z'^3-2(3x'yz')=2g(x',y,z').$

Tehát ha tudunk egy olyan középpontosan szimmetrikus konvex testet találni, melynek minden pontjára $\displaystyle g(x,y,z) < 1,5d$, és a térfogata legalább $\displaystyle 8d$, akkor készen vagyunk.

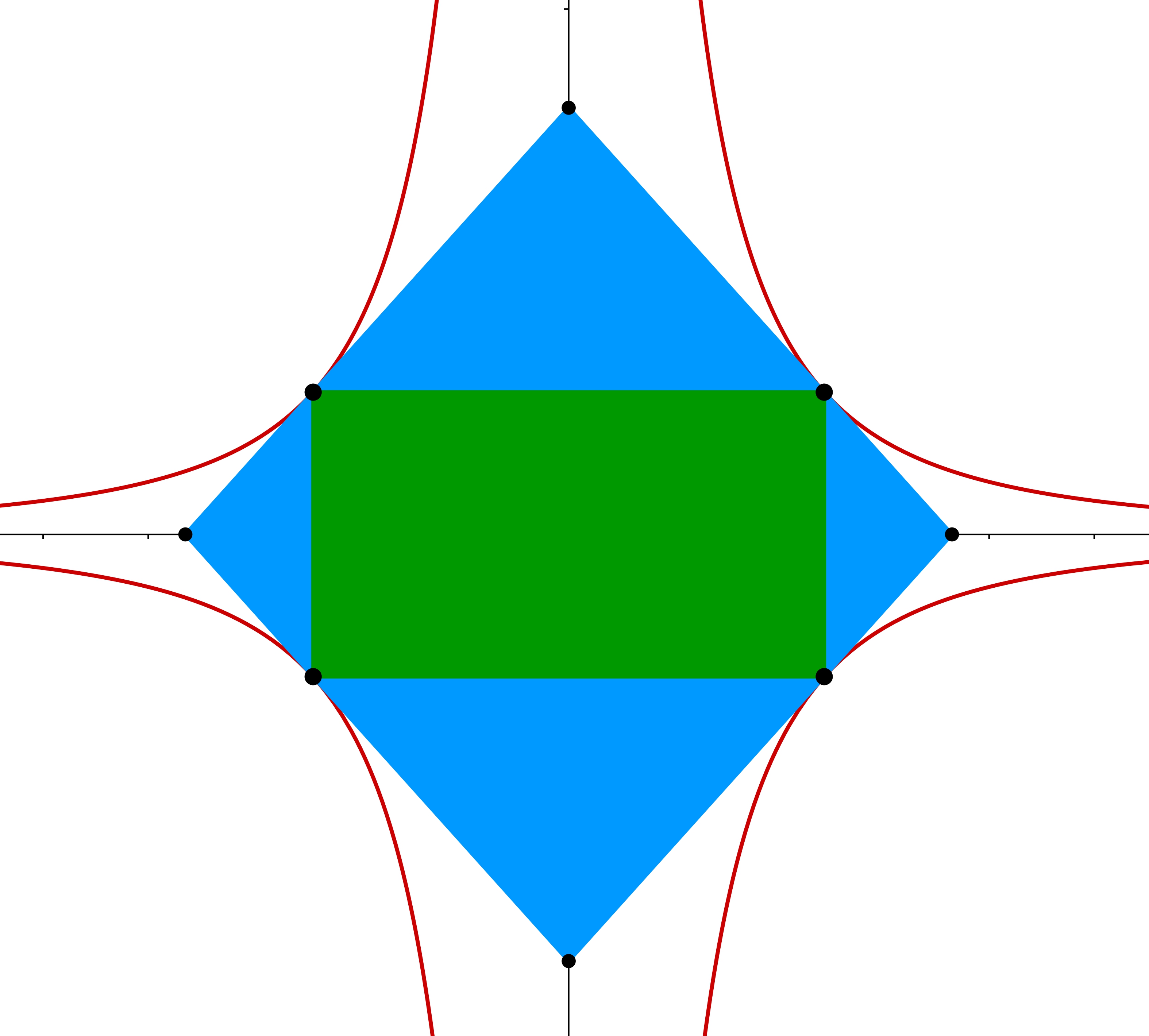
Bámulatos módon van geometriai jelentése $\displaystyle g(x,y,z)$-nek, ezt fogjuk most vizsgálni. Az $\displaystyle f_1(x,y,z)=\frac{(1,1,1)}{\sqrt{3}} \cdot (x,y,z)=\frac{x+y+z}{\sqrt3}$ skaláris szorzat pont az $\displaystyle (x,y,z)$ vektor $\displaystyle (1,1,1)$ vektorral párhuzamos komponense, ezért a Pitagorasz-tétel szerint az $\displaystyle (x,y,z)$ pont távolságának négyzete az $\displaystyle (1,1,1)$ irányú egyenestől:

$\displaystyle f_2(x,y,z)^2=x^2+y^2+z^2-\left(\frac{x+y+z}{\sqrt3}\right)^2= \frac{2}{3} (x^2+y^2+z^2-xy-yz-zx).$

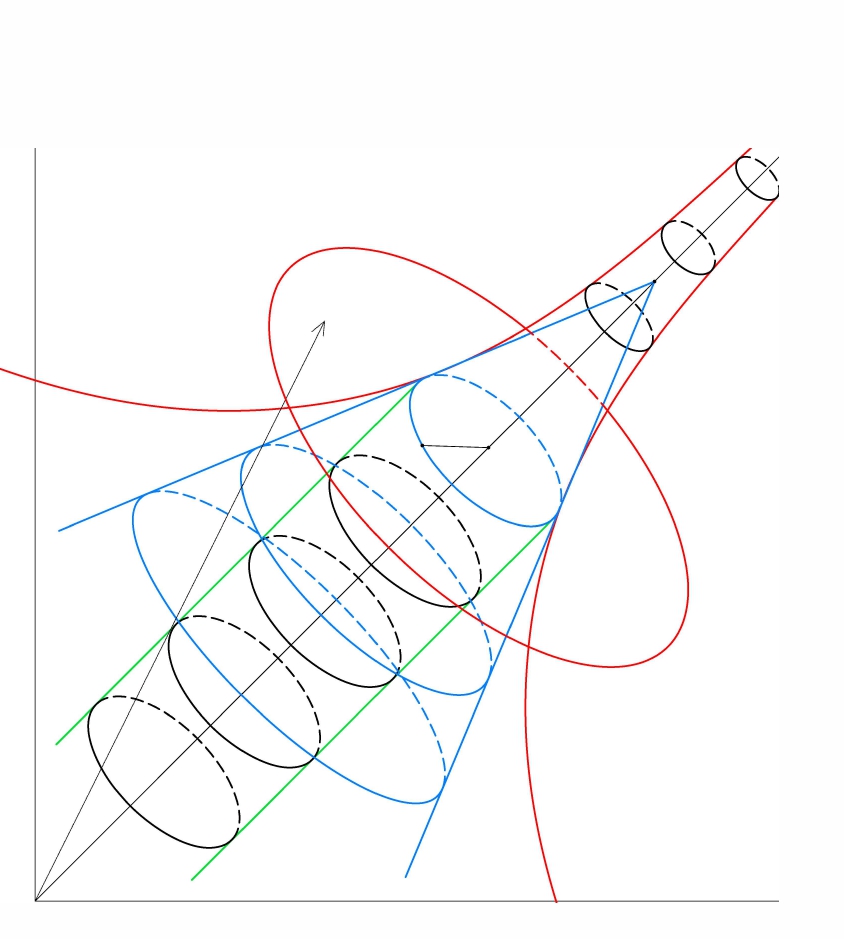
Ez már egy szorzótényezője $\displaystyle g(x,y,z)$-nek, szóval mi lesz a geometriai jelentése annak, ha ezt még megszorozzuk $\displaystyle f_1(x,y,z)$-vel? Ha ügyesek vagyunk akkor pont egy térfogat, méghozzá az alábbi testé: vesszük a pontot, körbeforgatjuk az $\displaystyle (1,1,1)$ irányú egyenes körül, ez egy kör, tükrözzük az origóra, és az így kapott két körlap konvex burkát nézve egy hengert kapunk, amelynek a térfogata:

$\displaystyle 2 \cdot f_1(x,y,z) \cdot \pi \cdot f_2(x,y,z)^2=2 \cdot \frac{x+y+z}{\sqrt 3} \cdot \pi \cdot \frac{2}{3} (x^2+y^2+z^2-xy-yz-zx) = g(x,y,z) \frac{4\pi}{3 \sqrt 3}.$

Szóval ha veszünk egy $\displaystyle P$ pontot a $\displaystyle g(x,y,z)=1,5d$ felületen, mondjuk $\displaystyle P=\frac{\sqrt[3]{3d}}{2}(1,1,2)$-t, és tekintjük a fenti hengert, akkor a térfogata $\displaystyle g(P)\frac{4\pi}{3 \sqrt 3}=\frac{2\pi\cdot d}{\sqrt{3}}$, ami nem elég nagy ahhoz hogy megkapjuk az állítást. Viszont ha tekintünk egy ,,duplakúpot'', amely tartalmazza a hengert és érinti a $\displaystyle g(x,y,z)=1,5d$ felületet, akkor elég nagy térfogatot kapunk. A részletek kidolgozásához legyen $\displaystyle K_P$ azon pontok halmaza, amelyre

$\displaystyle \left|\frac{1}{3}\cdot \frac{f_1(x,y,z)}{f_1(P)}\right|+\left|\frac{2}{3}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|<1.$

Minden $\displaystyle (x,y,z)\in K_P$ pontra felírható a számtani-mértani alapján:

$\displaystyle \left|\frac{g(x,y,z)}{g(P)}\right|=\left|\frac{f_1(x,y,z)}{f_1(P)}\cdot \frac{f_2(x,y,z)}{f_2(P)}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|\leq \left(\left|\frac{1}{3}\cdot \frac{f_1(x,y,z)}{f_1(P)}\right|+\left|\frac{2}{3}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|\right)^3<1$

Az $\displaystyle f_1$ és az $\displaystyle f_2$ geometriai jelentése miatt $\displaystyle K_P$ egy duplakúp, azaz közzéppontosan szimmetrikus és konvex, valamint minden $\displaystyle (x,y,z)\in K_P$-re $\displaystyle g(x,y,z)<g(P)=1.5k$. $\displaystyle K_p$ "magassága" az origótól véve $\displaystyle 3f_1(P)$, és az alapkörének sugara $\displaystyle \frac{3}{2}f_2(P)$, ezért a térfogata

$\displaystyle 2\cdot \frac{(3f_2(P)/2)^2\cdot (3f_1(P))\cdot \pi}{3}=g(P) \frac{3\pi}{\sqrt 3}=1,5d\cdot \frac{3\pi}{\sqrt 3}$

Ez pedig nagyobb, mint $\displaystyle 8d$, hiszen mindkettőt négyzetre emelve $\displaystyle \pi^2 > \frac{256}{27}$ adódik, ami igaz, azaz készen vagyunk.

Keresztmetszeti ábra:

Vázlatrajz:

Statisztika:

11 dolgozat érkezett.
7 pontot kapott:	Bodor Mátyás, Diaconescu Tashi, Holló Martin, Varga Boldizsár.
6 pontot kapott:	Forrai Boldizsár, Minh Hoang Tran, Szakács Ábel.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. novemberi matematika feladatai