 |
Az A. 894. feladat (2024. december) |
A. 894. Az ABCDE konvex poliéder olyan, hogy a DE szakasz az ABC háromszög síkját a háromszög belsejében metszi el. Forgassuk el a D pontot az AB, BC, CA egyenesek körül kifelé az ABC síkba; a kapott pontok legyenek D1, D2 és D3. Hasonlóan, az E pontot is forgassuk az ABC síkba az AB, BC, CA egyenesek körül kifelé; a kapott pontok legyenek E1, E2 és E3.
Mutassuk meg, hogy ha a poliédernek van beírt gömbje, akkor a D1D2D3 és az E1E2E3 háromszögek köréírt körei koncentrikusak.
Javasolta: Kós Géza (Budapest)
(7 pont)
A beküldési határidő 2025. január 10-én LEJÁRT.
Megoldás. Legyen a poliéderbe beírt gömb G, érintési pontjai az ABD, BCD, CAD, BAE, CBE, ACE síkokon rendre T1, T2, T3, U1, U2, illetve U3.
I. Bár nyilvánvalónak tűnhet, gondoljuk meg, hogy a beírt gömb érintési pontjai a lapok belsejébe esnek. Legyen a G középpontja I. Ez a pont a poliéder lapszögfelező síkjain van, ezért például az ABI, ADI és BDI háromszögek az ABD lappal hegyesszöget zárnak be.

A T1 pont az I merőleges vetülete az ABD síkon, ez a pont az AB, BD, DA egyeneseknek az ABD háromszöget tartalmazó oldalán, tehát mindenképpen az ABD háromszög belsejében van. Hasonlóan láthatjuk, hogy a T2 pont a BCD, a T3 pont a CAD, U1 a BAE, U2 a CBE, az U3 pont pedig az ACE háromszög belsejébe esik.
II. A Ti és Ui pontoknak a megfelelő tengely körül az ABC síkba forgatott képeit jelölje T′i, illetve U′i (i=1,2,3). Megmutatjuk, hogy T′i=U′i mindegyik i-re.

A kifelé forgatás miatt T′1 az ABD1 háromszög belsejében, U′1 pedig az ABE1 háromszög belsejében, tehát mindkettő az AB egyenesnek a C-vel ellentétes oldalán van. A G-hez húzott egyenlő érintők miatt AT′1=AT1=AU1=AU′1 és BT′1=BT1=BU1=BU′1, tehát az ABT′1 és a ABU′1 háromszögek egybevágók; de ez csak úgy lehet, ha T′1=U′1. Hasonlóan láthatjuk, hogy T′2=U′2 és T′3=U′3.
III. Legyen az ABCD tetraéder ABC laphoz hozzáírt gömbje GD, érintési pontjai az ABC, ABD, BCD, CAD síkokon rendre P0, P1, P2, illetve P3. Azt állítjuk, hogy a D1D2D3 és a T′1T′2T′3 körök koncentrikusak, a közös középpontjuk a P0 pont.
A G és GD gömböket egy D középpontú nagyítás viszi egymásba, ezért mindegyik Ti pont a megfelelő DPi szakasz belsejébe esik. A D pontból a gömbökhöz húzott érintő szakaszok egyenlők, így
DT1=DT2=DT3,DP1=DP2=DP3ésT1P1=T2P2=T3P3.
Az ABD lapnak az ABD1 háromszögbe forgatását helyettesíthetjük az ABCD tetraéder AB-re fektetett külső lapszögfelező síkjára való tükrözéssel, ekkor tehát D tükörképe D1, T1 tükörképe T′1, és P1 tükörképe P0. Ugyanígy, a D, T2, P2 pontoknak az BC élhez tartozó külső lapszögfelező síkra vonatkozó tükörképei D2, T′2, illetve P0, végül az D, T3, P3 pontoknak a CA-hoz tartozó külső lapszögfelező síkra való tükörképei D3, T′3, illetve P0.
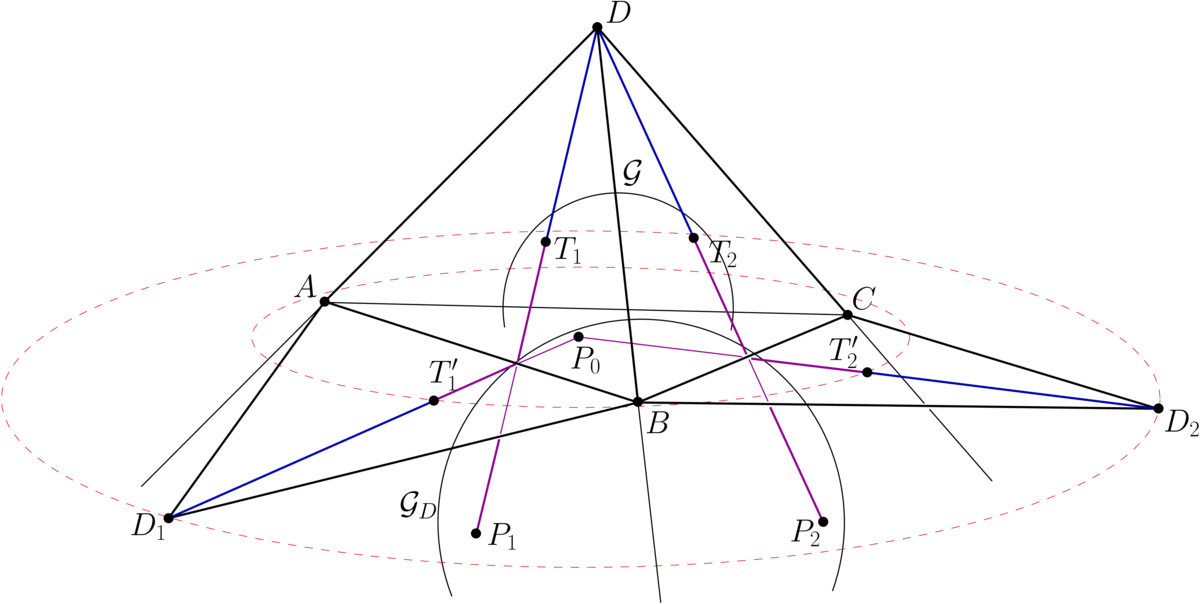
A tükrözések miatt
D1P0=DP1,D2P0=DP2ésD3P0=DP3,
T′1P0=T1P1,T′2P0=T2P2ésT′3P0=T3P3.
Azt már láttuk, hogy DP1=DP2=DP3 és T1P1=T2P2=T3P3, így D1P0=D2P0=D3P0 és T′1P0=T′2P0=D′3P0; a D1D2D3 és a T′1T′2T′3 kör középpontja is P0.
IV. Az előző pont szerint a D1D2D3 és T′1T′2T′3 körök koncentrikusak. Az ABCE tetraédernek az ABC laphoz hozzáírt gömbje segítségével ugyanígy igazolhatjuk, hogy az E1E2E3 kör koncentrikus az U′1U′2U′3 körrel. Mivel azonban a T′1T′2T′3 és az U′1U′2U′3 kör azonos, a D1D2D3 és az E1E2E3 kör egymással is koncentrikus, és az is igaz, hogy a két hozzáírt gömb ugyanabban a pontban érinti az ABC háromszöglapot.
Megjegyzés. A megoldás a hozzáírt gömbök nélkül is elmondható.
Mivel BT′1=BT1=BT2=BT′2, D1B=DB=D2B és D1T′1=DT1=DT2=D2T′2, a BT′1D1 és BT′2D2 háromszögek egybevágók, és mivel T′1 az ABD1, T′2 pedig az CBD2 háromszögnek belső pontja, az irányításuk ellentétes.
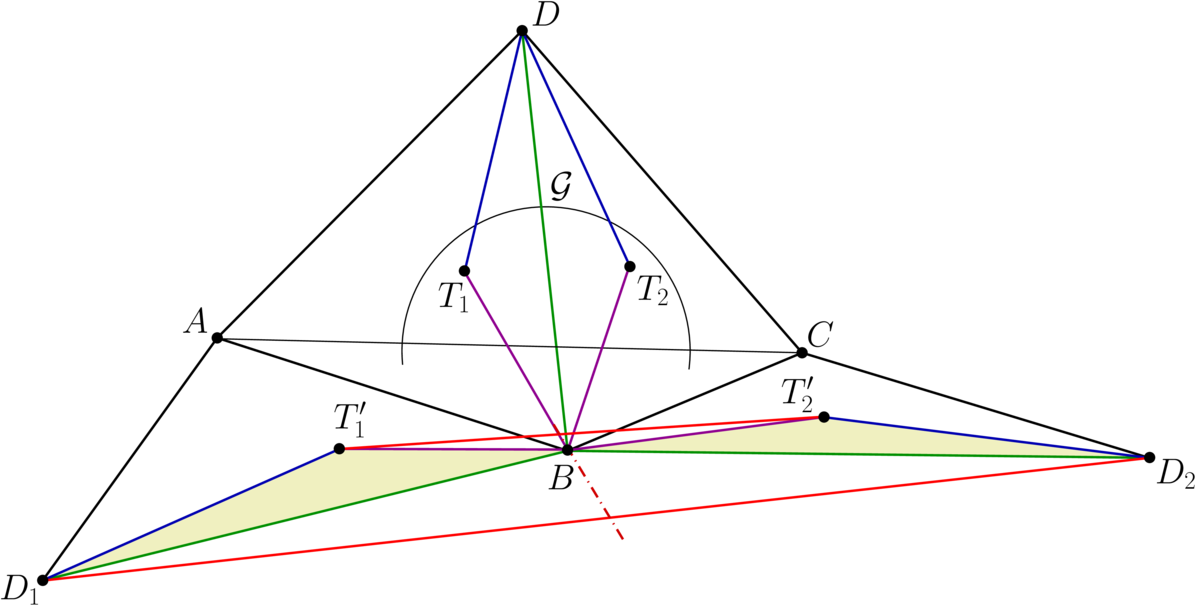
Ezért a D1D2T′2T′1 négyszög szimmetrikus trapéz, a szimmetriatengelye a D1D2 és T′1T′2 alapok közös felezőmerőlegese. Ugyanez a D2D3T′3T′2 és D3D1T′1T′3 négyszögekről is elmondható. A közös oldalfelező merőlegesek miatt a D1D2D3 és T′1T′2T′3 háromszögek köré írt körök középpontja ugyanaz.
Statisztika:
12 dolgozat érkezett. 7 pontot kapott: Aravin Peter, Bodor Mátyás, Forrai Boldizsár, Gyenes Károly, Holló Martin, Keresztély Zsófia, Szakács Ábel, Varga Boldizsár, Vödrös Dániel László, Xiaoyi Mo. 4 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2024. decemberi matematika feladatai
|
|

