 |
Az A. 902. feladat (2025. március) |
A. 902. Az ABC háromszög belsejében lévő D pont olyan, hogy a BCD háromszög szabályos. Legyen E a D pont izogonális konjugáltja. Jelölje P azt a pontot az AB félegyenesen, amelyre |AP|=|BE|. Hasonlóan, jelölje Q azt a pontot az AC félegyenesen, amelyre |AQ|=|CE|. Mutassuk meg, hogy az AD egyenes felezi a PQ szakaszt.
Javasolta: Bán-Szabó Áron (Budapest)
(7 pont)
A beküldési határidő 2025. április 10-én LEJÁRT.
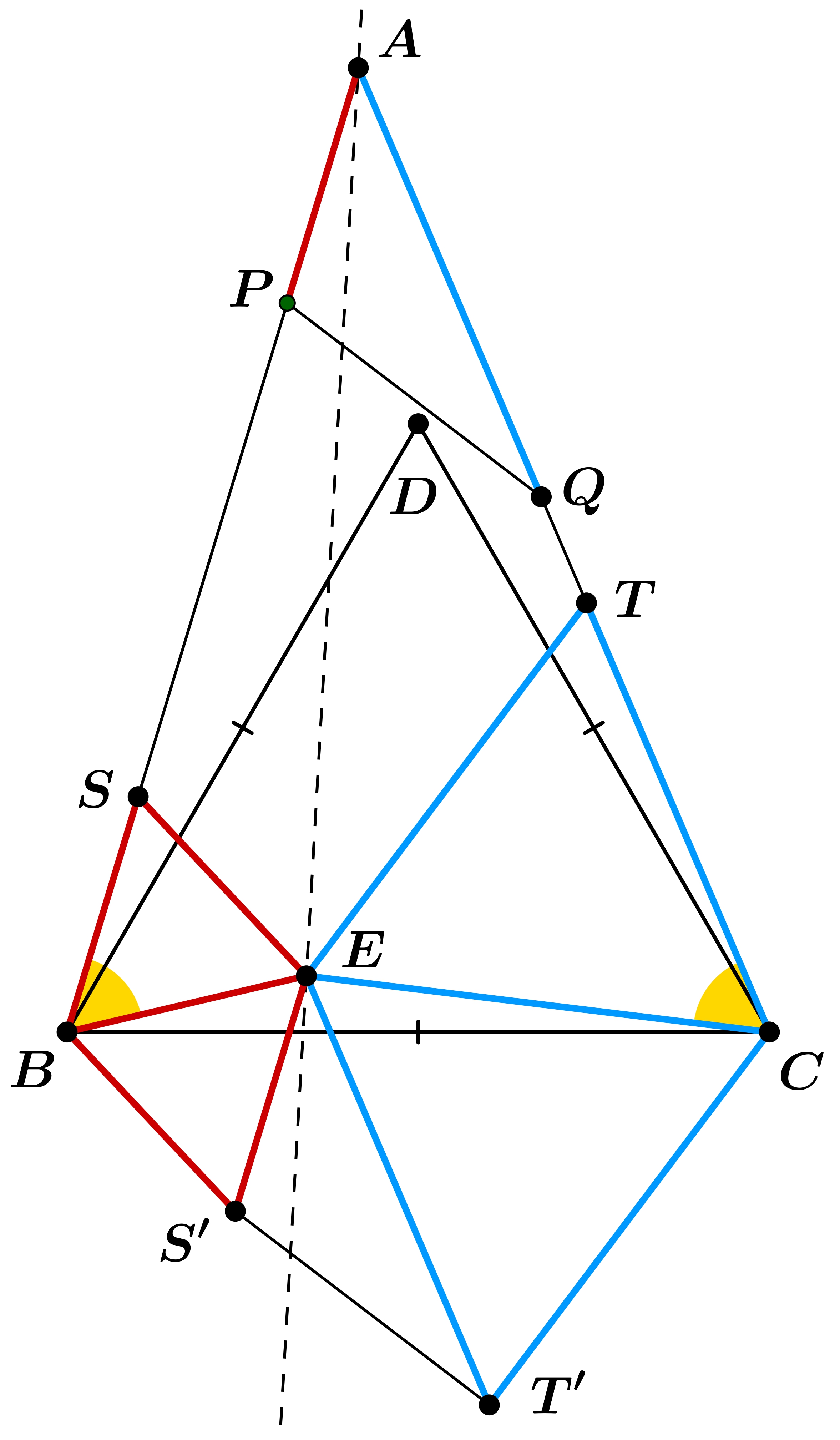
Első megoldás (szimmediánokkal): A BA,CA félegyeneseken vegyük fel rendre az S,T pontokat úgy, hogy BS=BE és CT=CE teljesüljenek. Mivel EBA∢=EBS∢=ECA∢=ECT∢=60∘, a BES és CET háromszögek szabályosak. Vegyük fel az S′ és T′ pontokat úgy, hogy a BSES′ és CTET′ négyszögek paralelogrammák legyenek, tehát úgy, hogy a BES′ és CET′ háromszögek is szabályosak legyenek. Vegyük észre, hogy az ES′,SB,AP szakaszok párhuzamosak és egyenlő hosszúak. Hasonlóan, az ET′,TC,AQ szakaszok is párhuzamosak és egyenlő hosszúak, így az APQ háromszöget az →AE vektorral eltolva az ES′T′ háromszöget kapjuk. Az eredeti bizonyítandó állítás az, hogy az AD egyenes felezi a PQ szakaszt. Ez ekvivalens azzal, hogy az AE egyenes szimmedián az APQ háromszögben, hiszen az AD és AE egyenesek izogonálisak. Az eltolás ezen nem változtat, így elég azt igazolni, hogy az AE egyenes szimmedián az ES′T′ háromszögben. Ismert, hogy egy háromszögben egy csúcshoz tartozó szimmedián azon pontok mértani helye, amelyre a közbezáró oldalaktól való távolságok aránya egyenlő a közbezáró oldalak arányával (kicsit pontosítva két ilyen egyenes létezik, és nekünk az az egyenes kell, ami átmegy a háromszögön). Tehát elég azt igazolni, hogy d(A,ES′)/d(A,ET′)=ES′/ET′, ahol d a távolságfüggvény. Viszont d(A,ES′)=d(AB,ES′)=d(SB,ES′) hiszen az AB,ES′ egyenesek párhuzamosak, ez pedig a szabályos háromszögek miatt éppen √32⋅ES′. Hasonlóan d(A,ET′)=d(AC,ET′)=d(TC,ET′)=√32⋅ET′, így valóban d(A,ES′)/d(A,ET′)=ES′/ET′. Készen vagyunk.
Második megoldás (mozgatásokkal): Fel fogunk használni egy ismert lemmát:
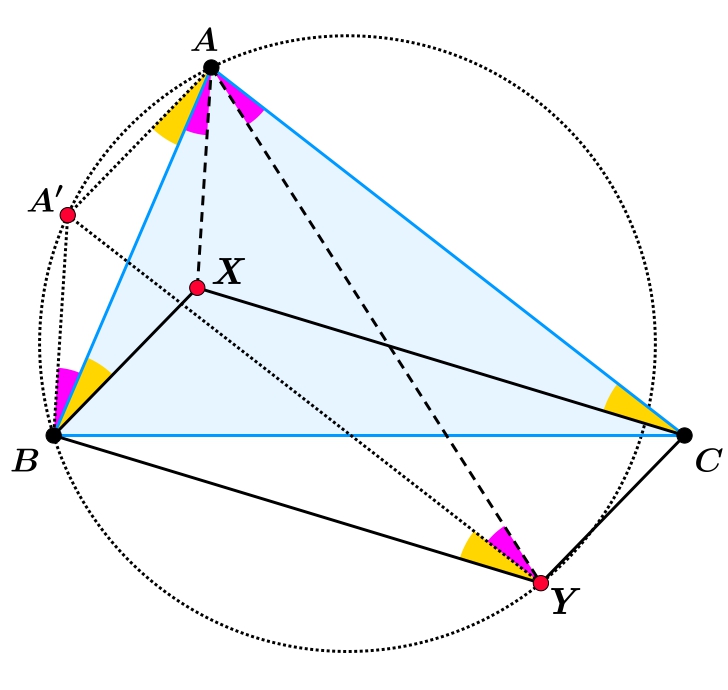
Lemma: Adott egy ABC háromszög (nem a feladatbeli), benne pedig egy X pont, amire XBA∢=ACX∢. Legyen Y az a pont, melyre BXCY paralelogramma. Ekkor az X,Y pontok A-izogonálisak. Bizonyítás: Legyen A′ az a pont, melyre az AXBA′ és ACYA′ négyszögek paralelogrammák. Ekkor A′AB∢=XBA∢=ACX∢=A′YB∢, hiszen AC∥A′Y és XC∥BY. Így az A,A′,B,Y pontok egy körön vannak. Ezt felhasználva kapjuk, hogy BAX∢=ABA′∢=AYA′∢=YAC∢. Ezzel a lemmát beláttuk.
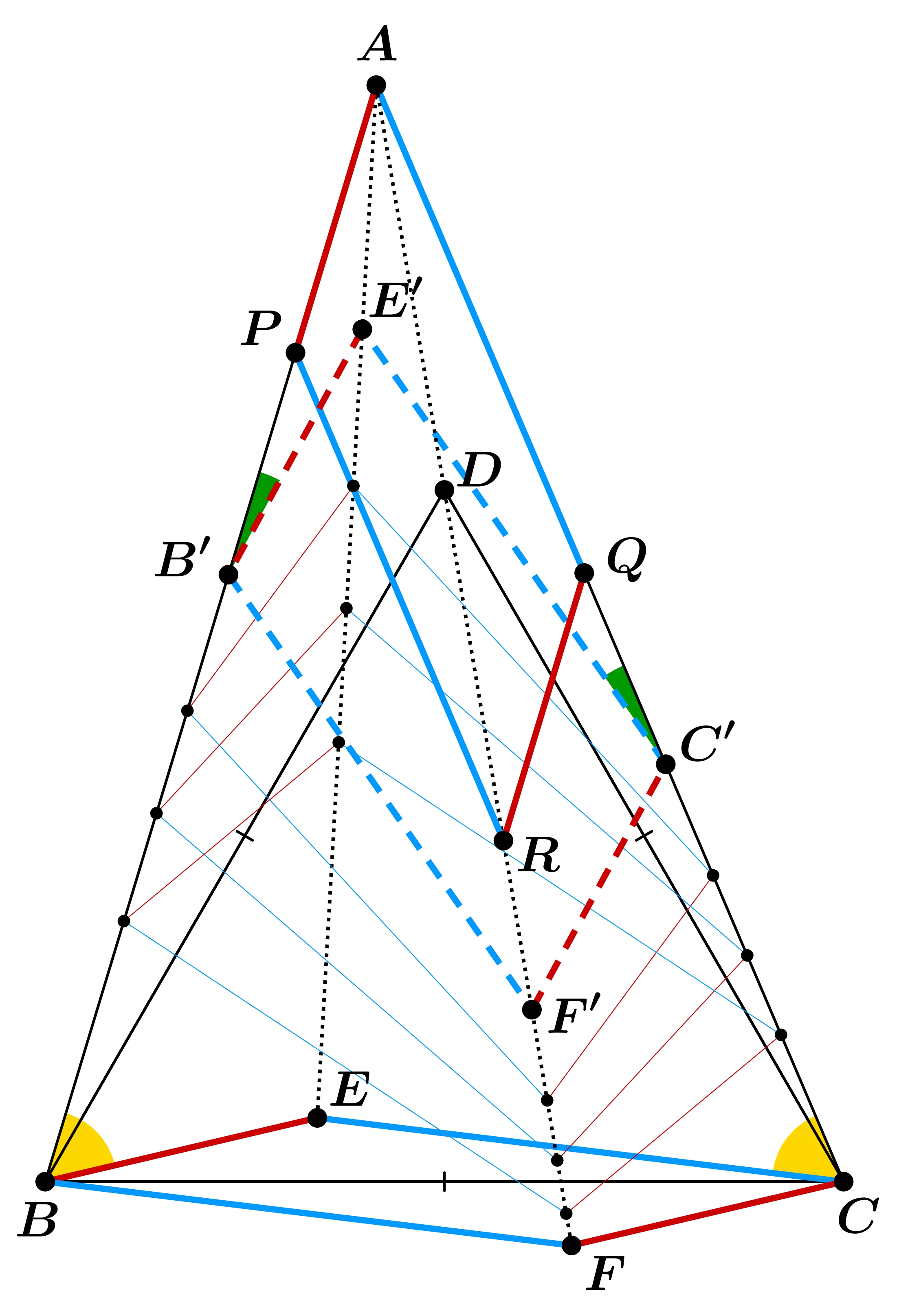
Most térjünk rá a feladatra. Jelölje F az E pont tükörképét a BC oldal felezőpontjára, míg jelölje R az A pont tükörképét a PQ felezőpontjára. Mivel EBA∢=DBC∢=60∘=BCD∢=ACE∢, használhatjuk a lemmánkat, és azt kapjuk, hogy az AE,AF egyenesek A-izogonálisak. De mivel az AD,AE egyenesek is azok, elég belátni, hogy az A,R,F pontok egy egyenesen vannak.
Képzeljük el, hogy egy fizikai modellt építünk a feladathoz. A BECF paralelogramma oldalaira gondoljunk úgy, mintha pálcák lennének, melyek hossza állandó. Az AB,AC félegyenesekre gondoljunk sínekként, amin a B,C pontok mozognak. Így ha az E pontot kicsit mozgatjuk, akkor is egy olyan paralelogrammánk lesz, aminek oldalai BE és CE hosszúak, továbbá az egyik szemközti csúcspárja az AB,AC síneken van. Elég azt bebizonyítani, hogy ahogy az E csúcsot behúzzuk lineárisan A-ba, úgy az F pont is lineárisan tart A-felé, hiszen amikor E elmegy A-ba, akkor B elmegy P-be, C elmegy Q-ba és F elmegy R-be.
Tegyük fel, hogy amint húzzuk E-t A-ba, egyszer csak megállunk. Legyen ekkor a BECF paralelogramma képe a B′E′C′F′ paralelogramma. Tudjuk, hogy az A−B−B′, A−C−C′, A−E−E′ ponthármasok kollineárisak. Azt szeretnénk belátni, hogy az A−F−F′ pontok is egy egyenesen vannak, ami ekvivalens azzal, hogy az AE′,AF′ egyenesek A-izogonálisak. Ehhez a lemmát szeretnénk használni az AB′C′ háromszögben az E′ pontra. Ehhez arra lenne szükség, hogy E′B′A∢=AC′E′∢ teljesüljön. Használjuk fel az ismert állítást, miszerint ha két háromszögnek egy-egy oldala egyenlő hosszú, és az azzal szemközti szögek is egyenlőek, akkor a háromszögek körülírt körei egybevágóak (kerületi szögek tétele miatt). Illetve fordítva is majdnem ugyanez az állítás, ha két háromszögnek egybevágóak a körülírt körei, illetve van egy-egy ugyanolyan hosszú oldaluk, akkor ezen oldalakkal szemközti szögek vagy egyenlőek, vagy 180∘-ra egészítik ki egymást. Az ABE,AB′E′ háromszögekre BE=B′E′ és az A-nál lévő szögük közös, így a körülírt körei egybevágóak. Az ABE,ACE háromszögek AE oldala közös, és az azzal szemközti szögek mind 60 fokosak, így körülírt körei egybevágóak. Végül az ACE,AC′E′ háromszögekre is CE=C′E′ és az A-nál lévő szögük közös, így körülírt körei egybevágóak. Ezzel azt kaptuk, hogy az AB′E′,AC′E′ háromszögek körülírt körei egybevágóak. Ám az AE′ oldal közös, és könnyen látszik, hogy AB′E′∢+E′C′A∢≠180∘, így valóban E′B′A∢=AC′E′∢. Ezzel beláttuk az állítást.
Már csak egy dolgot kell átgondolni: a fenti gondolatmenet nem érvényes akkor, amikor E=A. Viszont ahogy lineárisan húzzuk E-t A-ba, F az AF egyenesen fog mozogni, így a folytonosság miatt ha E-val tartunk A-ba, akkor az F olyan pontba tart, ami rajta lesz az AF egyenesen. Készen is vagyunk.
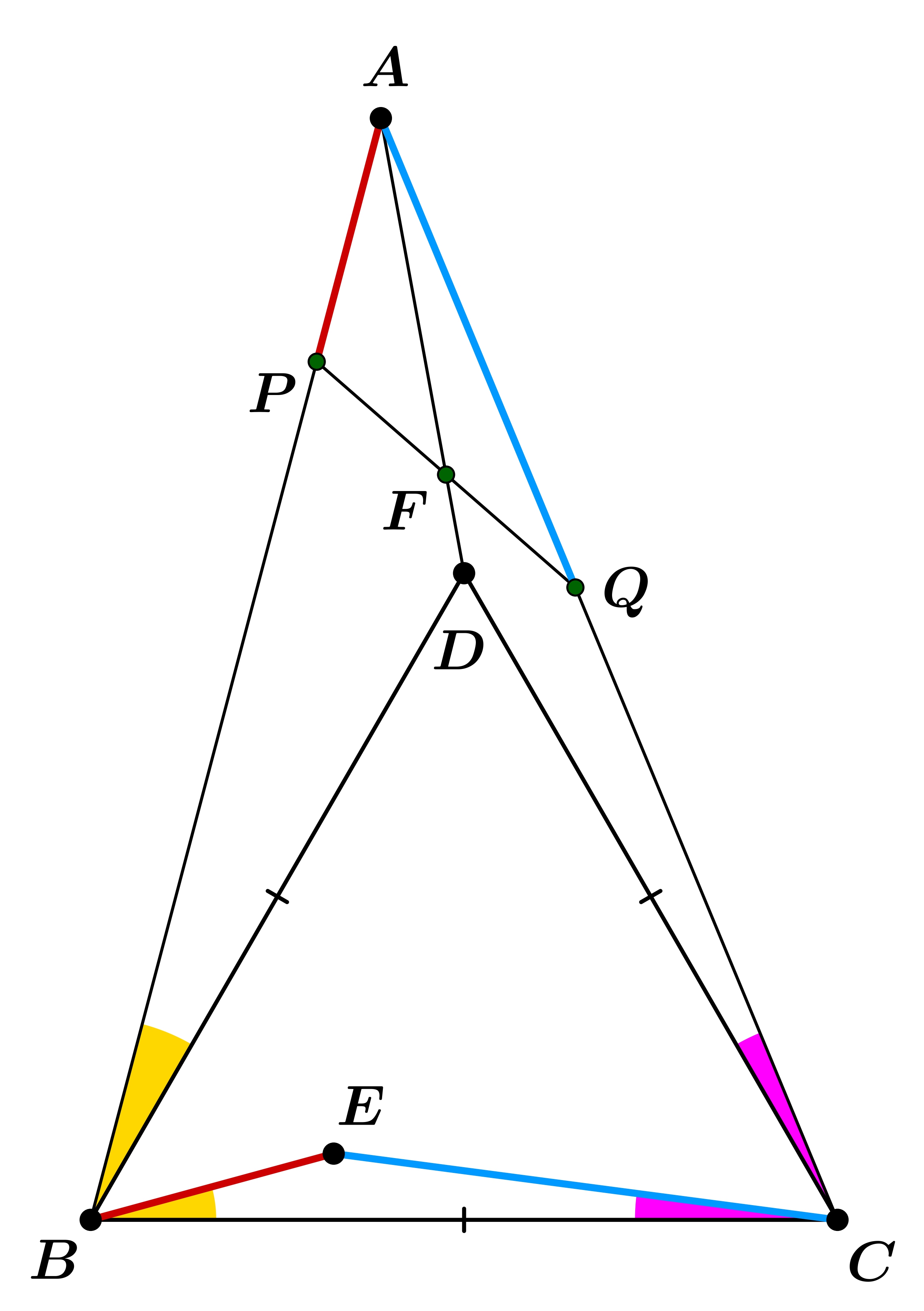
Harmadik megoldás (szinusz-tétellel): Jelölje a PQ és AD egyenesek metszéspontját F. Azt szeretnénk igazolni, hogy PF=FQ. Alkalmazzuk a szinusz-tételt az APF és AFQ háromszögekben:
PF=AF⋅sinPAF∢sinFPA∢,FQ=AF⋅sinFAQ∢sinAQF∢.
Tehát elég azt igazolnunk, hogy sinPAF∢sinFPA∢=sinFAQ∢sinAQF∢, amit átrendezve a sinAQF∢sinFPA∢=sinFAQ∢sinPAF∢ bizonyítandóhoz jutunk.
Az APQ háromszögben felírt szinusz-tétel szerint, és használva, hogy AP=BE és AQ=CE,
BECE=APAQ=sinAQP∢sinQPA∢=sinAQF∢sinFPA∢.
Tehát arra vezettük vissza a feladat állítását, hogy BECE=sinFAQ∢sinPAF∢.
Most alkalmazzuk a szinusz-tételt a BEC háromszögben, és használjuk ki az izogonális konjugálás definícióját, miszerint CBE∢=DBA∢ és ECB∢=ACD∢. Azt kapjuk, hogy
BECE=sinECB∢sinCBE∢=sinACD∢sinDBA∢.
Ezzel a bizonyítandót a sinFAQ∢sinPAF∢=sinACD∢sinDBA∢ azonosságra vezettük vissza, amit átrendezve, és azonos szögeket beírva, a sinDAC∢sinACD∢=sinBAD∢sinDBA∢ egyenletet kapjuk.
Használva, hogy a BCD szabályossága miatt BD=CD, a bizonyítandó következik az ACD és ADB háromszögekben felírt szinusz-tételekből:
sinDAC∢sinACD∢=CDAD=BDAD=sinBAD∢sinDBA∢.
Ezzel a bizonyítást befejeztük.
Statisztika:
14 dolgozat érkezett. 7 pontot kapott: Aravin Peter, Bodor Mátyás, Bui Thuy-Trang Nikolett, Czanik Pál, Forrai Boldizsár, Holló Martin, Keresztély Zsófia, Sha Jingyuan, Szakács Ábel, Varga Boldizsár, Virág Tóbiás. 6 pontot kapott: Tianyue DAI, Xiaoyi Mo. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. márciusi matematika feladatai
|
|

