 |
A B. 3821. feladat (2005. április) |
B. 3821. Az a, b, c pozitív számokra a2+b2+c2=1. Határozzuk meg az
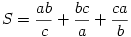
összeg legkisebb lehetséges értékét.
(5 pont)
A beküldési határidő 2005. május 17-én LEJÁRT.
Megoldás. Állítjuk, hogy S2 3(a2+b2+c2), vagyis hogy
3(a2+b2+c2), vagyis hogy
Ezzel ekvivalens, hogy
(a2b2+b2c2+c2a2)2 3a2b2c2(a2+b2+c2),
3a2b2c2(a2+b2+c2),
ami átrendezés után az
a4b4+b4c4+c4a4 a4b2c2+b4c2a2+c4a2b2
a4b2c2+b4c2a2+c4a2b2
alakot ölti. További átrendezés során látható, hogy az
egyenlőtlenséget kell igazolnunk, ami nyilvánvaló.
Vagyis S2 3, ahol egyenlőség csakis az a2=b2=c2 esetben állhat fönn. Az S összeg legkisebb lehetséges értéke tehát
3, ahol egyenlőség csakis az a2=b2=c2 esetben állhat fönn. Az S összeg legkisebb lehetséges értéke tehát , mely értéket
esetén veszi fel.
Statisztika:
79 dolgozat érkezett. 5 pontot kapott: 52 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 22 versenyző.
A KöMaL 2005. áprilisi matematika feladatai
|
|

