Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A B. 3829. feladat (2005. május)

B. 3829. Legyenek a1, a2, ..., an pozitív számok. Igazoljuk, hogy

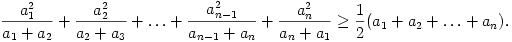
\frac{a_1^2}{a_1+a_2}+\frac{a_2^2}{a_2+a_3}+\ldots+\frac{a_{n-1}^2}{a_{n-1}+a_n}+ \frac{a_n^2}{a_n+a_1}\ge\frac{1}{2}(a_1+a_2+\ldots+a_n).

(5 pont)

A beküldési határidő 2005. június 15-én LEJÁRT.

Megoldás. Tekintsük az

{a_2^2\over a_1+a_2}+{a_3^2\over a_2+a_3}+\ldots+{a_{n}^2\over a_{n-1}+a_n}+ {a_1^2\over a_n+a_1}

összeget, ezt a baloldali összegből kivonva az eredmény

{a_1^2-a_2^2\over a_1+a_2}+{a_2^2-a_3^2\over a_2+a_3}+\ldots+ {a_{n-1}^2-a_{n}^2\over a_{n-1}+a_n}+ {a_n^2-a_1^2\over a_n+a_1}=

=(a_1-a_2)+(a_2-a_3)+\ldots+(a_{n-1}-a_n)+(a_n-a_1)=0.

Vagyis elegendő az eredetivel ekvivalens

{a_1^2+a_2^2\over a_1+a_2}+{a_2^2+a_3^2\over a_2+a_3}+\ldots+ {a_{n-1}^2+a_{n}^2\over a_{n-1}+a_n}+ {a_n^2+a_1^2\over a_n+a_1} \ge a_1+a_2+\ldots+a_{n-1}+a_n

egyenlőtlenséget igazolni. Azonban tetszőleges pozitív a,b esetén

{a^2+b^2\over a+b}\ge {a+b\over 2},

hiszen átszorzás után a 2(a2+b2)\ge(a+b)2 egyenlőtlenséget kapjuk, ami ekvivalens az (a-b)2\ge0 egyenlőtlenséggel, és az is látható, hogy egyenlőség csak az a=b esetben áll fenn. Ha ezt az egyenlőtlenséget összegezzük az összes olyan a,b párra, ahol a=ai és b=ai+1, az an+1=a1 jelöléssel élve, akkor éppen a bizonyítandó egyenlőtlenséget kapjuk, és az is kiderül, hogy egyenlőség pontosan akkor áll fenn, ha a_1=a_2=\ldots=a_n.

Statisztika:

67 dolgozat érkezett.
5 pontot kapott:Békéssy Herman András, Blázsik Zoltán, Bogár 560 Péter, Cseh Ágnes, Csorba János, Dömötör Erika, Dücső Márton, Estélyi István, Fegyverneki Dániel, Fischer Richárd, Gehér György, Gombkötő Tamás, Gyenizse Gergő, Haszpra Tímea, Hujter Bálint, Kálosi Anna, Kardos Kinga Gabriela, Kisfaludi-Bak Sándor, Kiss-Tóth Christian, Komáromy Dani, Kovács 129 Péter, Kunovszki Péter, Kutas Péter, Lorántfy Bettina, Maros Máté Előd, Mátyás Péter, Mészáros Gábor, Nagy 224 Csaba, Nagy-Baló András, Nándori Balázs, Németh 007 Zsolt, Peregi Tamás, Pesti Veronika, Poronyi Balázs, Sárkány Lőrinc, Sümegi Károly, Szabó 308 Zsolt, Szalóki Dávid, Szilágyi Dániel, Tomon István, Tossenberger Anna, Tóth 666 László Márton, Udvari Balázs, Varga 111 Péter, Vörös 174 Eszter.
4 pontot kapott:16 versenyző.
3 pontot kapott:1 versenyző.
2 pontot kapott:1 versenyző.
0 pontot kapott:4 versenyző.

A KöMaL 2005. májusi matematika feladatai