 |
A B. 3969. feladat (2007. január) |
B. 3969. Mi egy hegyesszögű háromszög köré írt szabályos háromszögek középpontjainak halmaza? (A G háromszög a H köré van írva, ha H csúcsai a G oldalaira illeszkednek.)
(5 pont)
A beküldési határidő 2007. február 15-én LEJÁRT.
Megoldás: Ha a H háromszög szabályos, akkor az összes köré írható szabályos háromszög középpontja egybeesik H középpontjával, a továbbiakban tehát feltehetjük, hogy H-nak van 60o-tól eltérő szöge. Ha H-nak egyetlen 60o-nál kisebb szöge van, akkor pontosan három olyan köré írt G szabályos háromszög létezik, amelynek valamelyi oldalára H-nak két csúcsa is illeszkedik, nevezetesen H bármely oldalegyenesére illeszthető egy alkalmas G háromszög. Ha viszont H-nak két 60o-nál kisebb szöge is van, akkor csak két ilyen G található, a leghosszabb oldal egyenesére nem illeszthetünk alkalmas G-t.
Vizsgáljuk tehát azokat a G=DEF szabályos háromszögeket, amelyeknek DE oldalára a H=ABC háromszög A csúcsa, EF oldalára a B csúcs, FD oldalára pedig C illeszkedik. Ekkor D,E és F rendre a CA, AB, illetve BC oldalak fölé kifelé írt 60o-os kD, kE, kF látóköríven helyezkednek el, ezek középpontját jelölje rendre OD, OE, OF. Vegyünk fel egy G'=D'E'F' háromszöget is hasonló tulajdonsággal, és vizsgáljuk meg, hogy származtatható G-ből G'. Ha az EBE' irányított szög nagysága  , akkor nyilván az FBF', FCF', DCD', DAD' és EAE' irányított szögek is
, akkor nyilván az FBF', FCF', DCD', DAD' és EAE' irányított szögek is  -vel egyenlők. A kerületi és középponti szögek között fennálló összefüggés alapján tehát a D,E és F pontokat rendre OD, OE, illetve OF köröli 2
-vel egyenlők. A kerületi és középponti szögek között fennálló összefüggés alapján tehát a D,E és F pontokat rendre OD, OE, illetve OF köröli 2 szögű forgatás viszi a D', E', F' pontokba.
szögű forgatás viszi a D', E', F' pontokba.
Legyen S az OD,OE,OF háromszög súlypontja (ez a háromszög amúgy szabályos, de ez a feladat szempontjából mellékes körülmény). Jelölje  az S körüli 2
az S körüli 2 szögű forgatást. A S pontból a D, E, F, D', E', F', OD, OE, OF pontokba mutató vektorokat jelölje rendre d, e, f, d', e', f', x, y, z. Ekkor d'=
szögű forgatást. A S pontból a D, E, F, D', E', F', OD, OE, OF pontokba mutató vektorokat jelölje rendre d, e, f, d', e', f', x, y, z. Ekkor d'= (d-x)+x, e'=
(d-x)+x, e'= (e-y)+y, f'=
(e-y)+y, f'= (f-z)+z, és x+y+z=0. Mivel egy szabályos háromszög középpontja egyben a súlypontja is, S-ből a G' háromszög középpontjába mutató vektor
(f-z)+z, és x+y+z=0. Mivel egy szabályos háromszög középpontja egyben a súlypontja is, S-ből a G' háromszög középpontjába mutató vektor
vagyis a G háromszög középpontját S középpontú, 2 szögű elforgatás viszi a G' háromszög középpontjába. Az összes ilyen általános helyzetben H köré írt szabályos háromszög középpontja tehát egy S középpontú (esetleg 0 sugarú) körvonalon helyezkedik el, méghozzá a pontok egy folytonos nyílt körívet alkotnak.
szögű elforgatás viszi a G' háromszög középpontjába. Az összes ilyen általános helyzetben H köré írt szabályos háromszög középpontja tehát egy S középpontú (esetleg 0 sugarú) körvonalon helyezkedik el, méghozzá a pontok egy folytonos nyílt körívet alkotnak.
Erről a körívről a feladat diszkussziója során kaphatunk egy kicsit pontosabb képet. Nézzük először azt az esetet, amikor H-nak két 60o-nál kisebb szöge van. Legyen az A-nál, illetve a C-nél lévő szög 60o-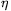 és 60o-
és 60o- , a B-nél lévő szög pedig 60o+
, a B-nél lévő szög pedig 60o+ , ahol 0<
, ahol 0< =
=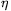 +
+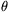 <30o. Az AB és CB egyenesek messék a kF, illetve kE látóköríveket az FB és EB pontokban, ekkor az EBAB és FBCB szögek nagysága egyaránt
<30o. Az AB és CB egyenesek messék a kF, illetve kE látóköríveket az FB és EB pontokban, ekkor az EBAB és FBCB szögek nagysága egyaránt  , az E pont nem lehet az EBB íven, az F pont pedig nem lehet az FBB íven. Az EBA és FBC egyenesek kD-vel alkotott metszéspontja legyen DA, illetve DC, ekkor a DACA és DCAC szögek nagysága rendre
, az E pont nem lehet az EBB íven, az F pont pedig nem lehet az FBB íven. Az EBA és FBC egyenesek kD-vel alkotott metszéspontja legyen DA, illetve DC, ekkor a DACA és DCAC szögek nagysága rendre  -
-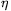 és
és  -
- . A D pont nem lehet sem az ADA, sem a CDC íven, az ADC és CDA egyenesek pedig érintik a kE,kF köröket az EA=A, illetve FC=C pontban. A DCDA ív egy tetszőleges D pontjából kiindulva kaphatunk tehát egy alkalmas G=DEF háromszöget úgy, hogy E az EAEB, F pedig az FBFC ívre esik. Más lehetőség nincs, az ívek végpontjai pedig az első bekezdésben leírt két speciális G háromszöghöz tartoznak. Mindhárom ívhez, és így a G háromszögek középpontjait alkotó zárt körívhez is 240o-2
. A D pont nem lehet sem az ADA, sem a CDC íven, az ADC és CDA egyenesek pedig érintik a kE,kF köröket az EA=A, illetve FC=C pontban. A DCDA ív egy tetszőleges D pontjából kiindulva kaphatunk tehát egy alkalmas G=DEF háromszöget úgy, hogy E az EAEB, F pedig az FBFC ívre esik. Más lehetőség nincs, az ívek végpontjai pedig az első bekezdésben leírt két speciális G háromszöghöz tartoznak. Mindhárom ívhez, és így a G háromszögek középpontjait alkotó zárt körívhez is 240o-2 >180o nagyságú középponti szög tartozik.
>180o nagyságú középponti szög tartozik.
A másik esetben, ha az A, B, C csúcsoknál lévő szögek nagysága rendre 60o+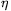 , 60o-
, 60o- és 60o+
és 60o+ , ahol 0
, ahol 0
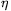 ,
, <30o és 0<
<30o és 0< =
=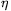 +
+ <60o, hasonló helyzet áll elő, csak most EB=FB=B, a DA, DC pontokat a BA, illetve BC egyeneseknek kD-vel alkotott metszéspontjaiként kapjuk, az EA, FC pontok pedig rendre a DCA és DAC egyeneseknek a kE, illetve kF körívvel alkotott metszéspontjai. A különbség annyi, hogy most az egyes ívekhez tartozó középponti szög 240o-2
<60o, hasonló helyzet áll elő, csak most EB=FB=B, a DA, DC pontokat a BA, illetve BC egyeneseknek kD-vel alkotott metszéspontjaiként kapjuk, az EA, FC pontok pedig rendre a DCA és DAC egyeneseknek a kE, illetve kF körívvel alkotott metszéspontjai. A különbség annyi, hogy most az egyes ívekhez tartozó középponti szög 240o-2 >120o lesz, a három speciális elhelyezkedésű G háromszög közül pedig kettő tartozik csak az ívek végpontjaihoz, a harmadik háromszög középpontja egy olyan pont lesz, ami a többi megoldást alkotó körívnek nem pontja.
>120o lesz, a három speciális elhelyezkedésű G háromszög közül pedig kettő tartozik csak az ívek végpontjaihoz, a harmadik háromszög középpontja egy olyan pont lesz, ami a többi megoldást alkotó körívnek nem pontja.
Végül vizsgáljuk meg, hogy - az esetlegesen egy izolált ponttól eltekintve - a G háromszögek középpontjának mértani helyét alkotó körív sugara lehet-e nulla. Tegyük fel, hogy ez a helyzet. Az EAEB ívhez tartozó középponti szög mindkét esetben nagyobb, mint 120o, ezért találhatók olyan G,G' háromszögek, hogy  =60o, vagyis a háromszögek egymást metsző oldalai 60o-os szöget zárnak be egymással. Feltevésünk esetén ez azt jelentené, hogy a G' háromszöget megkaphatjuk G-ből egy S középpontú, negatív arányú nagyítással, amiből DD'=EE'=FF' következne, vagyis a kD, kE, kF körök sugara megegyezne, tehát a H háromszög szabályos lenne.
=60o, vagyis a háromszögek egymást metsző oldalai 60o-os szöget zárnak be egymással. Feltevésünk esetén ez azt jelentené, hogy a G' háromszöget megkaphatjuk G-ből egy S középpontú, negatív arányú nagyítással, amiből DD'=EE'=FF' következne, vagyis a kD, kE, kF körök sugara megegyezne, tehát a H háromszög szabályos lenne.
Statisztika:
13 dolgozat érkezett. 5 pontot kapott: Wolosz János. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2007. januári matematika feladatai
|
|

