 |
A B. 4061. feladat (2008. január) |
B. 4061. Adott az ABC és a PQR háromszög úgy, hogy az A pont felezi a QR, a P pont a BC oldalt. A QR egyenes felezi a BAC, a BC egyenes a QPR szöget. Bizonyítsuk be, hogy
AB+AC=PQ+PR.
(5 pont)
A beküldési határidő 2008. február 15-én LEJÁRT.
Megoldás: Az ABC háromszög köré írható kört jelölje kA, a PQR háromszög köré írhatót pedig kP. A BC egyenesnek a kP körrel alkotott második metszéspontja legyen P', a QR egyenesnek kA-val alkotott második metszéspontja pedig A'. Mivel QPP' =RPP'
=RPP' , kapjuk, hogy QP'=RP', vagyis AP' éppen a QR szakasz felezőmerőlegese. Hasonlóképpen BA'=CA', és PA' éppen a BC szakasz felezőmerőlegese.
, kapjuk, hogy QP'=RP', vagyis AP' éppen a QR szakasz felezőmerőlegese. Hasonlóképpen BA'=CA', és PA' éppen a BC szakasz felezőmerőlegese.
Legyen AP'P =
= ,P'AB
,P'AB =
=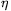 . Mivel CAA'
. Mivel CAA' =BAA'
=BAA' =90o-
=90o-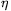 , kapjuk, hogy CAP'
, kapjuk, hogy CAP' =180o-
=180o-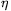 , és így BA'A
, és így BA'A =BCA
=BCA =
=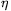 -
- . Továbbá CA'A
. Továbbá CA'A =CBA
=CBA =
= +
+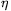 , ahonnan CA'P
, ahonnan CA'P =BA'P
=BA'P =
=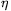 , PA'A
, PA'A =
= következik. Innen látszik, hogy az A',P,A,P' pontok egy k körvonalra illeszkednek, valamint hogy ha az A'P és P'A egyenesek metszéspontját T-vel jelöljük, akkor A'TA
következik. Innen látszik, hogy az A',P,A,P' pontok egy k körvonalra illeszkednek, valamint hogy ha az A'P és P'A egyenesek metszéspontját T-vel jelöljük, akkor A'TA =90o-
=90o- =BAA'
=BAA' +BCA
+BCA =BCA'
=BCA' +BCA
+BCA =A'CA
=A'CA . A T pont tehát illeszkedik a kA körre, és ugyanígy a kP körre is, méghozzá TA' a kA körnek, míg TP' a kP körnek átmérője is egyben.
. A T pont tehát illeszkedik a kA körre, és ugyanígy a kP körre is, méghozzá TA' a kA körnek, míg TP' a kP körnek átmérője is egyben.

A Ptolemaiosz-tétel szerint (PQ+PR)RP'=PQ.RP'+PR.QP'=QR.PP'=2AR.TP'cos  . Felhasználva a P'AR és P'RT derékszögű háromszögek hasonlóságát, innen
. Felhasználva a P'AR és P'RT derékszögű háromszögek hasonlóságát, innen
adódik, és ugyanígy AB+AC=2.TC.cos  . A bizonyítandó állításhoz elegendő tehát a TR=TC egyenlőséget igazolni.
. A bizonyítandó állításhoz elegendő tehát a TR=TC egyenlőséget igazolni.
Tegyük fel, hogy az XY és ZV szakaszok az M pontban metszik egymást. Jól ismert, hogy az X,Z,Y,V pontok pontosan akkor illeszkednek egy körvonalra, ha MX.MY=MZ.MV. Ezt rendre a kA, k és kP körökre alkalmazva
MB.MC=MA.MA'=MP.MP'=MQ.MR
adódik vagyis a B,Q,C és R pontok egy körre esnek. TB=TC és TQ=TR miatt ennek a körnek éppen T a középpontja, vagyis valóban TR=TC.
Statisztika:
8 dolgozat érkezett. 5 pontot kapott: Blázsik Zoltán, Dinh Hoangthanh Attila, Lovas Lia Izabella, Tossenberger Anna, Varga 171 László. 4 pontot kapott: Somogyi Ákos. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2008. januári matematika feladatai

