 |
A B. 4118. feladat (2008. október) |
B. 4118. Felbontható-e a zárt körlap két diszjunkt, egybevágó ponthalmaz egyesítésére? (A zárt körlap a körvonal pontjait is tartalmazza.)
(5 pont)
A beküldési határidő 2008. november 17-én LEJÁRT.
Megoldás: A kérdésre a válasz nemleges, amit indirekt fogunk bizonyítani. Tegyük fel, hogy a K körlap előáll az egymáshoz diszjunkt A és B halmazok egyesítéseként,  pedig a síknak olyan egybevágósága, amely A-t B-be viszi. A
pedig a síknak olyan egybevágósága, amely A-t B-be viszi. A  leképezés inverzét jelölje
leképezés inverzét jelölje 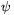 , ez tehát a síknak olyan egybevágósága, amely B-t A-ba viszi. Előrebocsátjuk, hogy
, ez tehát a síknak olyan egybevágósága, amely B-t A-ba viszi. Előrebocsátjuk, hogy  a K halmaz egyetlen pontját sem hagyhatja helyben, hiszen egy olyan pont szükségképpen benne lenne A-ban vagy B-ben, de akkor mindkét halmazban benne lenne. Azt fogjuk megmutatni, hogy létezik K-nak olyan p pontja, amelyre mind
a K halmaz egyetlen pontját sem hagyhatja helyben, hiszen egy olyan pont szükségképpen benne lenne A-ban vagy B-ben, de akkor mindkét halmazban benne lenne. Azt fogjuk megmutatni, hogy létezik K-nak olyan p pontja, amelyre mind  (p), mind
(p), mind 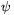 (p) a K körön kívül helyezkedik el. Mivel ekkor p sem az A, sem a B halmazhoz nem tartozhat, ellentmondásra jutunk.
(p) a K körön kívül helyezkedik el. Mivel ekkor p sem az A, sem a B halmazhoz nem tartozhat, ellentmondásra jutunk.
Tegyük fel először, hogy  irányítástartó. Minthogy helybenhagyás nyilván nem lehet, vagy egy nemnulla v vektorral történő eltolásról, vagy egy nemnulla szöggel történő elforgatásról van szó. Az első esetben legyen p a kör v-re merőleges átmérőjének egyik végpontja. Ha p
irányítástartó. Minthogy helybenhagyás nyilván nem lehet, vagy egy nemnulla v vektorral történő eltolásról, vagy egy nemnulla szöggel történő elforgatásról van szó. Az első esetben legyen p a kör v-re merőleges átmérőjének egyik végpontja. Ha p A, akkor p+v=
A, akkor p+v= (p)
(p) B a K körön kívül esik, ami lehetetlen, p
B a K körön kívül esik, ami lehetetlen, p B esetén pedig p-v=
B esetén pedig p-v=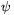 (p)
(p) A helyezkedne el a körön kívül. A másik esetben a forgatás o középpontja K-n kívül helyezkedik el, ekkor legyen p a kör o-tól legtávolabb eső pontja. Mind
A helyezkedne el a körön kívül. A másik esetben a forgatás o középpontja K-n kívül helyezkedik el, ekkor legyen p a kör o-tól legtávolabb eső pontja. Mind  (p), mind
(p), mind 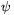 (p) a körön kívül esik, így megintcsak ellentmondásra jutunk.
(p) a körön kívül esik, így megintcsak ellentmondásra jutunk.
Tegyük fel végül, hogy  nem irányítástartó, ekkor vagy egy tükrözésről, vagy egy nemnulla v vektorral párhuzamos csúsztatva tükrözésről van szó. Az első esetben a
nem irányítástartó, ekkor vagy egy tükrözésről, vagy egy nemnulla v vektorral párhuzamos csúsztatva tükrözésről van szó. Az első esetben a  =
=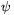 tükrözés tengelyének nem lehet közös pontja K-val, amiért is K bármely p pontja rendelkezik a fenti tulajdonsággal, a második esetben pedig válasszuk p-t a K körlap olyan pontjának, amely a csúsztatva tükrözés tengelyétől lehető legmesszebb esik.
tükrözés tengelyének nem lehet közös pontja K-val, amiért is K bármely p pontja rendelkezik a fenti tulajdonsággal, a második esetben pedig válasszuk p-t a K körlap olyan pontjának, amely a csúsztatva tükrözés tengelyétől lehető legmesszebb esik.
Statisztika:
73 dolgozat érkezett. 5 pontot kapott: Aujeszky Tamás, Blázsik Zoltán, Bodor Bertalan, Éles András, Énekes Péter, Fonyó Dávid, Kiss 902 Melinda Flóra, Lovas Lia Izabella, Márkus Bence, Mester Márton, Nagy 648 Donát, Somogyi Ákos, Varga 171 László, Varga 777 Ádám, Wang Daqian. 4 pontot kapott: Kunos Vid, Lelkes Ádám, Perjési Gábor, Weisz Ágoston. 3 pontot kapott: 7 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 44 versenyző.
A KöMaL 2008. októberi matematika feladatai
|
|

