A B. 4142. feladat (2009. január)

B. 4142. ,,850 darabos'' téglalap alakú kirakós játékunk igazából 851 darabból áll. Minden egyes darab az ábrán látható 5 mintadarab valamelyikével egyezik meg. Hány (E) típusú darab van a játékban?

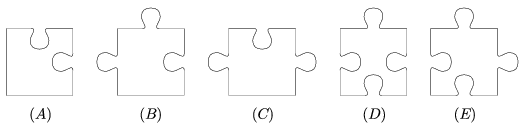
(4 pont)

A beküldési határidő 2009. február 16-án LEJÁRT.

Megoldás: Mivel 851=23^.37, ahol mindkét tényező prímszám, egy 23×37-es `puzzle'-ről van szó. Ennek a szélén 2(22+36)=116, belsejében pedig 851-116=735 darab helyezkedik el. A szélén lévő 116 darab közül a sarkokban helyezkedik el 4 darab (A) típusú, a maradék 112 pedig (B), illetve (C) típusú. Mivel minden `bemélyedés'-t egy `fül'-nek kell kitöltenie, világos, hogy minden oldalra pontosan egy (C) típusú darab kerül, a (B) típusú darabok száma pedig 108. A játék szélét összerakva tehát 104-gyel több fület látunk, mint bemélyedést. Így a belül elhelyezkedő (D), illetve (E) típusú darabokon a bemélyedések száma 104-gyel kell meghaladja a fülek számát. Ez azt jelenti, hogy a játékban 104/2=52 (D) típusú és 735-52=683 (E) típusú darab található.

Statisztika:

134 dolgozat érkezett.
4 pontot kapott:	84 versenyző.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2009. januári matematika feladatai