 |
A B. 4462. feladat (2012. szeptember) |
B. 4462. Egy doboz paprikásszalámis és egy doboz medvehagymás, nyolccikkelyes Maci-sajtot kiborítunk az asztalra, majd a 16 kis sajtot (címkéjükkel felfelé) visszatesszük a dobozokba. Hányféleképpen tehetjük ezt meg, ha a forgatással egymásba vihető elrendezéseket nem tekintjük különbözőnek, a két dobozt viszont megkülönböztetjük egymástól?
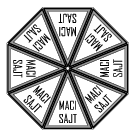
Javasolta: Koncz Levente (Budapest)
(4 pont)
A beküldési határidő 2012. október 10-én LEJÁRT.
Megoldás. Jelölje fn azon lehetőségek számát ahányféleképpen n darab paprikásszalámis és 8-n darab medvehagymás cikkelyt el tudunk rendezni egy dobozba úgy, hogy a forgatással egymásba vihető elrendezéseket nem tekintjük különbözőnek. Nyilván fn=f8-n és ha az első dobozba n darab paprikásszalámis sajt kerül, akkor a másodikba 8-n. Ezért a különböző lehetőségek száma
Nyilván f0=f1=1, továbbá f2=4, hiszen a két darab paprikásszalámis sajt között 0,1,2, vagy 3 hely maradhat ki. Azt sem nehéz megállapítani, hogy f3=7 és f4=10. Ha 3 darab paprikásszalámis sajt kerül a dobozba, akkor egy lehetőség az, hogy közvetlenül egymás mellett vannak, 4 olyan elrendezés van melyben kettő szomszédos, de a harmadik nem szomszédos egyikkel sem, és két olyan elrendezés van, amelyben semelyik kettő nem szomszédos. Ha pedig 4 darab paprikásszalámis sajt kerül a dobozba, akkor egy lehetőség az, hogy mind a 4 egymás mellett van, 3 olyan elrendezés van, melyben 3 egymás mellett van, de a negyedik nem, 3 olyan elrendezés van, melyben pontosan két sajt van, amelyik szomszédos, két olyan elrendezés van, melyben a sajtok két szomszédos párt alkotnak, és végül egy olyan elrendezés van, amelyben semelyik kettő nem szomszédos. Ezek szerint
L=2.(1+1+16+49)+100=234.
Statisztika:
232 dolgozat érkezett. 4 pontot kapott: 116 versenyző. 3 pontot kapott: 34 versenyző. 2 pontot kapott: 35 versenyző. 1 pontot kapott: 30 versenyző. 0 pontot kapott: 17 versenyző.
A KöMaL 2012. szeptemberi matematika feladatai
|
|

