 |
A B. 4553. feladat (2013. szeptember) |
B. 4553. Melyek azok a k pozitív egész számok, amelyekre 2.3k tökéletes szám?
(3 pont)
A beküldési határidő 2013. október 10-én LEJÁRT.
Megoldásvázlat. Az n=2.3k szám pozitív osztói az és a
számok; összegük, a mértani sorozat összegképletét felhasználva,
Az n szám akkor "tökéletes", ha 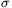 (n)=2n, azaz
(n)=2n, azaz
n=6=2.31.
Az egyetlen megoldás tehát a k=1.
Megjegyzés. Ismert, hogy a páros tökéletes számok a 2p-1(2p-1) alakú számok, ahol 2p-1 prím. A 2p-1 alakú prímszámokat Mersenne-prímnek nevezik.
Statisztika:
311 dolgozat érkezett. 3 pontot kapott: 229 versenyző. 2 pontot kapott: 25 versenyző. 1 pontot kapott: 38 versenyző. 0 pontot kapott: 19 versenyző.
A KöMaL 2013. szeptemberi matematika feladatai
|
|

