A B. 4760. feladat (2016. január)

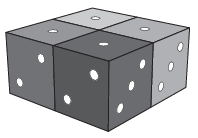
B. 4760. Négy különböző színű, szabályos dobókockát elhelyeztünk egymás mellett, az ábrán látható módon. Egy lépésben a következőt tehetjük: megfogunk két lapszomszédos kockát, és ezeket a közös lap középpontján átmenő, arra merőleges tengely körül $\displaystyle 90^\circ$-kal elforgatjuk. Hányféle különböző elrendezést lehet létrehozni ilyen lépésekkel?

(6 pont)

A beküldési határidő 2016. február 10-én LEJÁRT.

Megoldás. Jelöljük a (felülnézet szerinti) bal felső kocka lapjainak helyzetét 1, 2, 3, 4, 5, 6-tal, az 1-es a felső. Hasonlóan számozzuk a többi kocka lapjainak helyzetét is, a felül levők a 7-es, 13-as és a 19-es. Ha egy mozgatás során például a 1-es helyen levő lap a 2-esbe, az 2-es a 3-asbe, a 3-es pedig az 1-esbe kerül, továbbá a 4-es az 5-ösbe, az 5-ös a 6-osba, az pedig a 4-esba, akkor a mozgatást $\displaystyle (1,2,3)(4,5,6)$-tal jelöljük. Két mozgatás egymásutánját szorzatként jelöljük, egy $\displaystyle m$ mozgatás inverzét pedig jelölje $\displaystyle m^{-1}$. A négy tengely körüli 90°-os elforgatások az ábra szerint $\displaystyle a$, $\displaystyle b$, $\displaystyle c$ és $\displaystyle d$.

Ekkor

$\displaystyle a=(1,2,6,5)(7,8,12,11)\,,\, b=(1,4,6,3)(13,16,18,15)\,,$

$\displaystyle C:=aba^{-1}b^{-1}=(1,3,5)(2,6,4)\,,$

$\displaystyle D:=aabaab^{-1}=(1,6)(3,4)\,,$

$\displaystyle E:=abba^{-1}bb=(1,6)(2,5)\,, \text{így\ } DE=(2,5)(3,4)\,.$

Ezért

$\displaystyle DC=(1,4,5)(2,6,3) \,,\, DCD=(6,4,5)(2,1,3)\,,\, DCDDC=(1,2,4)(3,6,5)\,.$

A $\displaystyle C\,,\,D\,,\,E$ mozgatások és ezek szorzataiból előálló transzformációk csak a bal felső kocka lapjainak a helyzetét változtatják, ezek megfelelőivel hasonlóan változtatható bármelyik másik kocka helyzete is úgy, hogy a többié változatlan marad. Jelölje $\displaystyle G$ a bal felső kocka ilyen módon előálló összes különböző transzformációjának halmazát. Világos, hogy ezeknél az 1-es helyen levő lap a hat helyzet bármelyikébe eljuttatható. Ha $\displaystyle G_1$ azoknak a $\displaystyle G$-beli transzformációknak a halmaza, amelyek a felső lapot helybenhagyják, akkor könnyen látható, hogy $\displaystyle |G|=6\cdot|G_1|$. A $\displaystyle G_1$-beli mozgatások során az 1-essel szemköztes 6-os helyzetű lap is szükségképpen fixen marad, míg a 2-es a $\displaystyle DE$-nél az 5-ösbe megy. Így $\displaystyle |G_1|\geqslant 2\cdot|(G_1)_2|$, ezért $\displaystyle |G|\geqslant 6 \cdot 2=12$.

Másrészt az $\displaystyle abb=(1,2)(3,4)(5,6)(7,8,12,11)(13,18)(15,16)$ mozgatás hatása a bal felső kockán $\displaystyle (1,2)(3,4)(5,6)$, ami páratlan sok csere szorzataként $\displaystyle G$ minden elemétől különböző, ezért $\displaystyle G$ elemeit ezzel megszorozva $\displaystyle |G|$ számú egymástól és $\displaystyle G$ elemeitől különböző transzformációt kapunk - ezek a $\displaystyle G$ elemeivel együtt legalább $\displaystyle 12+12=24$ különböző helyzetbe állíthatják a bal felső kockát. Mivel összesen is csak ennyi térbeli mozgatás létezik, ami egy kockát önmagára képez, a bal felső kocka 24-féle helyzetet vehet föl. Az ehhez felhasznált transzformációknak a bal alsó kockára vonatkozó hatása vagy semmi, vagy $\displaystyle bb$-nek a hatása: $\displaystyle (13,18)(15,16)$, ami éppen $\displaystyle (1,6)(3,4)=D$ megfelelője. Így a bal alsó kocka is 24 különböző helyzetbe állítható a bal felső kocka bármelyik lehetséges helyzetéhez képest, és e helyzeteket megvalósító mozgatások hatása a jobb alsó kockára vagy semmi, vagy egy olyan transzformáció, ami a megengedett elforgatások olyan kombinációjával állítható vissza, ami a többi kockát nem befolyásolja. Ezért a jobb alsó kocka is 24 különböző helyzetet vehet föl, a bal oldali kockák helyzetétől függetlenül. A fennmaradó jobb felső kocka 12-féle helyzetbe állítható olyan forgatáskombinációkkal, amelyek a többi kocka helyzetét nem változtatják meg, tehát összesen $\displaystyle 24^3\cdot 12$-féle helyzetet elő tudunk állítani a fentiek szerint. Ez éppen a fele a négy kocka külön-külön történő bármilyen mozgatással kapható konfigurációk számának. Utóbbiaknak pontosan a fele a $\displaystyle 4\cdot 6=24$ laphelyzet páros permutációja, vagyis páros sok csere szorzataként kapható csak meg. Mivel mind a négy megengedett forgatás (így azok összes szorzata is) páros permutáció, a feladat kérdésére a válasz $\displaystyle 24^3\cdot 12$.

Statisztika:

34 dolgozat érkezett.
6 pontot kapott:	Baran Zsuzsanna, Bukva Balázs, Döbröntei Dávid Bence, Gáspár Attila, Imolay András, Klász Viktória, Kovács 246 Benedek, Lajkó Kálmán, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Nagy Kartal, Szabó 417 Dávid, Tóth Viktor, Váli Benedek.
5 pontot kapott:	Hansel Soma, Szabó Kristóf.
4 pontot kapott:	3 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	8 versenyző.

A KöMaL 2016. januári matematika feladatai