A B. 4825. feladat (2016. november)

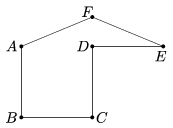
B. 4825. Vágjuk fel az ábrán látható konkáv hatszöget egy folytonos vágással két egybevágó darabra. Igazoljuk megoldásunk helyességét. (Az \(\displaystyle ABCD\) négyzet oldala egységnyi, az \(\displaystyle AEF\) egyenlőszárú háromszög alapja két egység, szárszöge \(\displaystyle 135^\circ\).)

(4 pont)

A beküldési határidő 2017. január 10-én LEJÁRT.

Megoldásvázlat. Az \(\displaystyle ABC\) derékszögű töröttvonalat forgassuk el \(\displaystyle C\) körül \(\displaystyle 90^{\circ}\)-kal az óramutató járásával megegyező irányban, így épp a \(\displaystyle CDE\) töröttvonalba kerül. Ez adja az ötletet, hogy próbálkozzunk a \(\displaystyle 45^{\circ}\)-os forgatottja mentén vágni. Csak azt kell meggondolni, hogy az \(\displaystyle A\) pont \(\displaystyle 45^{\circ}\)-kal elforgatott képe éppen \(\displaystyle F\), onnan a bizonyítás triviális.

Megjegyzés. Sokan elkövették azt a hibát, hogy nem bizonyították a felbontáskor kapott két ötszög egybevágóságának pontos feltételét. Sokan csak azt látták be, hogy a megfelelő szögek megegyeznek, és hogy egy oldalpár azonos hosszú – arra hivatkozva, hogy a szögek egyezősége miatt az alakzatok hasonlóak, és az azonos oldal miatt egybevágóak is. Ez az állítás háromszögeknél igaz, de nagyobb oldalszámú síkidomokra nem. (Könnyen látható, hogy például a téglalapokra nem igaz).

Statisztika:

87 dolgozat érkezett.
4 pontot kapott:	56 versenyző.
3 pontot kapott:	22 versenyző.
2 pontot kapott:	5 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2016. novemberi matematika feladatai