A B. 5041. feladat (2019. szeptember)

B. 5041. Egy $\displaystyle n \times n$-es táblázat mezőire egy-egy valós számot írunk. Egy ilyen táblázatot nullnégyzetnek hívunk, ha bármely legalább $\displaystyle 2 \times 2$-es négyzet alakú részében (így magában az egész táblázatban is) az elemek összege 0 (az ábrán egy $\displaystyle 3\times3$-as példa látható).

Mekkora a lehető legnagyobb $\displaystyle n$, amelyre van olyan $\displaystyle n \times n$-es nullnégyzet, amelynek nem minden mezőjén 0 áll?

(5 pont)

A beküldési határidő 2019. október 10-én LEJÁRT.

Megoldás. Először megmutatjuk, hogy $\displaystyle n=7$ esetén már nincs nemtriviális nullnégyzet, majd $\displaystyle n=6$ esetén adunk egy nemtriviális kitöltést.

Tekintsünk először egy $\displaystyle 4 \times 4$-es nullnégyzetet, és a mezőiben szereplő számokat jelöljük rendre $\displaystyle a_{1,1}, a_{1,2}, a_{1,3}, a_{1,4}, a_{2,1}, ..., a_{4,4}$-gyel.

Bevezetjük a következő jelölést: az $\displaystyle a_{i,j}$ és az $\displaystyle a_{i+k,j+k}$ sarokmezők által meghatározott nullnégyzetet az $\displaystyle \left(\left( a_{i,j};a_{i+k,j+k} \right) \right)$ módon fogjuk jelölni.
Az $\displaystyle \left(\left( a_{1,1};a_{3,3} \right) \right)$ $\displaystyle 3 \times 3$-as nullnégyzetnek az $\displaystyle a_{2,2}, a_{2,3}, a_{3,2}, a_{3,3}$ mezők által meghatározott $\displaystyle 2 \times 2$-es nullnégyzet a része, emiatt a kimaradó 5 elem összege 0, azaz $\displaystyle a_{1,1}+a_{1,2}+a_{1,3}+a_{2,1}+a_{3,1} = 0$.
Hasonlóan az $\displaystyle \left(\left( a_{2,2};a_{4,4} \right) \right)$ $\displaystyle 3 \times 3$-as nullnégyzetnek is része az $\displaystyle a_{2,2}, a_{2,3}, a_{3,2}, a_{3,3}$ mezők által meghatározott $\displaystyle 2 \times 2$-es nullnégyzet, azaz $\displaystyle a_{4,2}+a_{4,3}+a_{4,4}+a_{2,4}+a_{3,4} = 0$.
Másfelől mivel a kiinduló $\displaystyle 4 \times 4$-es nullnégyzetünkben is 0 az elemek összege és az ebben a négyzetben szereplő számok pontosan a középső $\displaystyle 2\times2$-es nullnégyzet, a két "oldalt kimaradó" 5-5 nulla összegű elem, illetve $\displaystyle a_{1,4}$ és $\displaystyle a_{4,1}$, ezért $\displaystyle a_{4,1} + a_{1,4} = 0$. Innen nyilvánvalóan következik, hogy egy legalább négy méretű nullnégyzetben az egymástól átlósan három távolságra lévő mezőpárok esetén ezen mezők számainak összege 0; azaz $\displaystyle a_{i,j}+a_{i+3,j+3}=0$, illetve $\displaystyle a_{i,j}+a_{i+3,j-3}=0$.
Nagyobb $\displaystyle (k+1) \times (k+1)$-es ($\displaystyle k>3$) nullnégyzetből kiindulva pontosan ugyanígy megmutatható, hogy az egymástól átlósan $\displaystyle k$ távolságra lévő mezőpárok esetén ezen mezők számainak összege is 0; azaz $\displaystyle a_{i,j}+a_{i+k,j+k}=0$, illetve $\displaystyle a_{i,j}+a_{i+k,j-k}=0$.

Ezek után vizsgáljunk egy $\displaystyle 5 \times 5$ méretű nullnégyzetet (a mezőket $\displaystyle a_{1,1}$-től $\displaystyle a_{5,5}$-ig jelöljük).
Az $\displaystyle \left(\left( a_{3,3};a_{5,5} \right) \right)$, valamint az $\displaystyle \left(\left( a_{4,4};a_{5,5} \right) \right)$ nullnégyzet volta miatt (az előzőekhez hasonlóan) a kimaradó 5 elem összegére: $\displaystyle a_{3,3}+a_{3,4}+a_{3,5}+a_{4,3}+a_{5,3}=0$.
Másfelől a teljes $\displaystyle 5 \times 5$-ös nullnégyzetünk előáll az $\displaystyle \left(\left( a_{1,1};a_{3,3} \right) \right)$, az $\displaystyle \left(\left( a_{1,4};a_{2,5} \right) \right)$, a $\displaystyle \left(\left( a_{4,1};a_{5,2} \right) \right)$ és a $\displaystyle \left(\left( a_{4,4};a_{5,5} \right) \right)$ nullnégyzetek, valamint a négy kimaradó $\displaystyle a_{3,4}, a_{3,5}, a_{4,3}, a_{5,3}$ mezők diszkrét uniójaként. Emiatt $\displaystyle a_{3,4}+a_{3,5}+a_{4,3}+a_{5,3}=0$ és így $\displaystyle a_{3,3}=0$, azaz egy $\displaystyle 5 \times 5$-ös nullnégyzet középső mezőjén csak 0 állhat.

Most már térjünk rá a $\displaystyle 7 \times 7$-es eset tárgyalására!
A $\displaystyle 7\times 7$-es nullnégyzet középső $\displaystyle \left(\left( a_{3,3};a_{5,5} \right) \right)$ 9 mezője közül valamennyi egy megfelelő $\displaystyle 5 \times 5$ méretű nullnégyzet középső mezője, azaz mindegyik helyen 0 áll.
Ezért a tőlük átlósan 3-ra lévő mezőkön is csak 0 állhat az $\displaystyle a_{i,j}+a_{i+3,j+3}=0$, illetve $\displaystyle a_{i,j}+a_{i+3,j-3}=0$ szabályok miatt; azaz a nagy nullnégyzet $\displaystyle \left(\left( a_{1,1};a_{2,2} \right) \right)$-es, $\displaystyle \left(\left( a_{6,1};a_{7,2} \right) \right)$ -es, $\displaystyle \left(\left( a_{1,6};a_{2,7} \right) \right)$-es és $\displaystyle \left(\left( a_{6,6};a_{7,7} \right) \right)$-es részeiben szintén minden szám 0.
Innen $\displaystyle a_{2,3}=a_{3,2}=a_{5,2}=a_{6,3}=a_{3,6}=a_{5,2}=a_{5,6}=a_{6,5}=0$, mert minden ilyen mező átlósan négy távolságra van az imént vizsgált $\displaystyle 2\times2$ méretű csupa 0 számot tartalmazó nullnégyzet egy-egy mezőjétől. (Például az $\displaystyle a_{1,2}=0$ mezőtől négy távol van az $\displaystyle a_{1+4,2+4} = a_{5,6}$ mező).
A még nem tárgyalt mezők esetén pedig rendre mindegyik mezőhöz van olyan $\displaystyle 2 \times 2$-es méretű nullnégyzet, amelynek három már ismert eleme mind 0, azaz a kimaradó mezők is mind 0-k.

Vagyis nincs nemtriviális $\displaystyle 7\times7$ méretű nullnégyzet.

A leírt bizonyítás lépéseit szemlélteti az alábbi ábra:

$\displaystyle n=6$ esetre pedig adható példa:

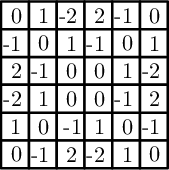
Azaz legfelejebb $\displaystyle 6 \times6$-os méretben létezik nemtriviális nullnégyzet.

Statisztika:

85 dolgozat érkezett.
5 pontot kapott:	58 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	13 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2019. szeptemberi matematika feladatai