A B. 5064. feladat (2019. december)

B. 5064. Az ábrán látható 26 mezőből álló ,,tábla'' hányféleképpen fedhető 13 ,,dominóval''? Egy-egy dominó két szomszédos mezőt fed le. (Az egymásba forgatható megoldásokat különbözőnek tekintjük.)

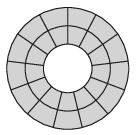
(4 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

Megoldás. Ha a már dominóval lefedett ábrát az egyetlen függőleges 2 hosszú szakasza mentén (azaz "12 óránál") elvágjuk, akkor két eset lehetséges: vagy nem vágunk el dominót, vagy pontosan két dominót vágunk el. Ugyanis, ha egyetlen dominót vágnánk ketté, akkor az kikényszerítené, hogy a 26 mező "külső" 13 mezejét és a "belső" 13 mezejét is úgy kellene lefednünk dominókkal, hogy minden dominó vagy két külső, vagy két belső mezőt fedne le, ami (mivel 13 nem páros) lehetetlen.

a) Ha nem vágunk el dominót. Az ábrát "kiterítve" $\displaystyle 13 \times 2$ méretű téglalapot kell lefednünk dominókkal. (Ez egy "klasszikus" Fibonacci feladat.)
Megmutatjuk, hogy tetszőleges $\displaystyle n \times 2$ méretű téglalapot $\displaystyle f_{n+1}$ féleképpen fedhetünk le (ahol $\displaystyle f_{n}$ az $\displaystyle f_1=f_2=1;f_{n+2}=f_n+f_{n+1}$ rekurzióval definiált Fibonacci-sorozat.)

Jelölje $\displaystyle l_n$ az $\displaystyle n \times 2$ méretű téglalap megfelelő lefedéseinek a számát. Az $\displaystyle 1 \times 2$ és a $\displaystyle 2 \times 2$ méretű téglalapokat nyilván $\displaystyle l_1=1$, illetve $\displaystyle l_2=2$ féleképpen fedhetjük le, míg, ha $\displaystyle n>2$, akkor az $\displaystyle n \times 2$ méretű téglalap esetén a bal felső sarokban lévő mezőt vagy egy álló dominóval fedjük le, és ekkor a maradék $\displaystyle (n-1) \times 2$ méretű téglalapot $\displaystyle l_{n-1}$-féleképpen fedhetjük le; vagy egy fekvő dominóval fedjük le, ami kikényszeríti, hogy ezen dominó alatt lévő két mezőt szintén egy fekvő dominóval fedjünk le, és ekkor a maradék $\displaystyle (n-2) \times 2$ méretű téglalap $\displaystyle l_{n-2}$-féleképpen fedhető le. Azaz ekkor $\displaystyle l_n=l_{n-1}+l_{n-2}$, ami (a fenti $\displaystyle l_1,l_2$ értékek mellett) azt jelenti, hogy a lefedések száma valóban $\displaystyle l_n=f_{n+1}$. Mivel most $\displaystyle n=13$, ezen az ágon $\displaystyle f_{14}= 377$ eset van.

b) Ha két dominót vágunk ketté. Ekkor a két szétvágott dominót az ábrából elhagyva és a maradék ábrát "kiterítve": $\displaystyle 11 \times 2$ méretű téglalapot kell lefednünk dominókkal.

Ez az az előző a) pont 2-vel kisebb méretben; azaz ekkor $\displaystyle f_{12} = 144$ eset van.

Tehát összesen $\displaystyle 377+144=\boxed{ \;521 \;}$ eset van.

Megjegyzés: Általában ha $\displaystyle 2n$ mezőnk van és $\displaystyle n$ páros, akkor $\displaystyle 2 + f_{n-1} + f_{n+1} = 2+L_n$ eset van, hiszen ekkor az is lehetséges, hogy 1 dominót vágunk ketté, és ilyenkor egyértelmű a többi dominó helye, míg ha $\displaystyle n$ páratlan, akkor $\displaystyle f_{n-1} + f_{n+1}=L_n$ eset van (ahol ($\displaystyle L_n$ az ún. Lucas-sorozat).

Statisztika:

107 dolgozat érkezett.
4 pontot kapott:	53 versenyző.
3 pontot kapott:	33 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2019. decemberi matematika feladatai