A B. 5077. feladat (2020. január)

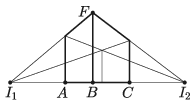
B. 5077. Egy kocka két iránypontos perspektív képét szeretnénk elkészíteni az ábra szerint. A két iránypont $\displaystyle I_1=(-9;0)$ és $\displaystyle I_2=(10;0)$; a kocka három csúcsának képe $\displaystyle A=(-3;0)$, $\displaystyle B=(0;0)$ és $\displaystyle C=(4;0)$. Mekkora legyen az $\displaystyle F$ pont $\displaystyle y$-koordinátája?

(6 pont)

A beküldési határidő 2020. február 10-én LEJÁRT.

Megoldás. Legyen $\displaystyle N$ a nézőpont, ahonnan a kockát a kép síkjára vetítjük.

Az $\displaystyle N$ pontból a kockát tetszőleges arányban nagyíthatjuk úgy, hogy közben a kép (az ablakra eső vetület) nem változik. Ezért feltételezhetjük, hogy a kocka $\displaystyle B$ csúcsa a kép síkjában van. A két iránypontos perspektíva azt jelenti, hogy a kép síkja függőleges, így az $\displaystyle F$ csúcs is a kép síkjában van.

Az $\displaystyle A,C$ pontok térbeli megfelelője legyen $\displaystyle A_1$, illetve $\displaystyle C_1$. Az $\displaystyle ABCN$ sík tartalmazza az $\displaystyle NAA_1$ és $\displaystyle NCC_1$ egyeneseket, tehát az $\displaystyle N$ pont az $\displaystyle A_1BC_1$ síkban, a kocka alaplapjának síkjában van. A két vízszintes fő irány az $\displaystyle NI_1$ és az $\displaystyle NI_2$, ezek párhuzamosak a kocka $\displaystyle BA_1$, illetve $\displaystyle BC_1$ élével.

Legyen a kocka élének hossza $\displaystyle d=BA_1=BC_1=BF$. A megadott adatok szerint $\displaystyle AI_1=6$, $\displaystyle AB=3$, $\displaystyle BC=4$, $\displaystyle CI_2=6$. A párhuzamos szelők tételéből $\displaystyle \frac{I_1N}{BA_1} = \frac{AI_1}{AB} = 2$, ezért $\displaystyle I_1N = 2\cdot BA_1 = 2d$. Hasonlóan, $\displaystyle \frac{I_2N}{BC_1} = \frac{CI_2}{BC} = \frac32$, ezért $\displaystyle I_2N = \tfrac32\cdot BC_1 = \tfrac32d$.

Az $\displaystyle I_1I_2N$ háromszög derékszögű, mert az $\displaystyle I_1N$ és az $\displaystyle I_2N$ oldala párhuzamos a kocka $\displaystyle BA_1$, illetve $\displaystyle BC_1$ éleivel. A Pitagorasz-tételt felírva

$\displaystyle 19^2 = {I_1I_2}^2 = {I_1N}^2 + {I_2N}^2 = (2d)^2+(\tfrac32d)^2 = (\tfrac52d)^2;$

ebből azt kapjuk, hogy $\displaystyle 19=\tfrac52d$, vagyis $\displaystyle d=\frac{38}{5}=7.6$.

A $\displaystyle BF$ él függőleges, a hossza $\displaystyle d=7,6$, tehát az $\displaystyle F$ pont képe a rajzon a $\displaystyle (0,7.6)$ pont.

Megjegyzés. A térbeli koordináta-rendszerben az $\displaystyle N$, $\displaystyle A_1$ és $\displaystyle C_1$ pontok koordinátái: $\displaystyle N=(3.16;0;9.12)$, $\displaystyle A_1=(-6.08;0;-4.56)$, $\displaystyle C_1=(4.56;0;-6.08)$.

Statisztika:

16 dolgozat érkezett.
6 pontot kapott:	Andó Viola, Baski Bence, Beke Csongor, Nádor Benedek, Németh Márton, Nguyen Bich Diep.
5 pontot kapott:	Hervay Bence, Lengyel Ádám.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2020. januári matematika feladatai