A B. 5114. feladat (2020. szeptember)

B. 5114. Az $\displaystyle ABCDEFGH$ egységkockát elmetszettük egy síkkal úgy, hogy az $\displaystyle AB$ és $\displaystyle AD$ éleket az $\displaystyle A$-tól azonos, $\displaystyle x$ távolságra levő $\displaystyle P$ és $\displaystyle Q$ belső pontjaikban, a $\displaystyle BF$ élt pedig az $\displaystyle R$ pontban metszi. Mekkora a $\displaystyle BR$ távolság, ha $\displaystyle QPR\sphericalangle=120^\circ$?

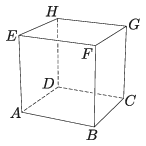
(4 pont)

A beküldési határidő 2020. október 12-én LEJÁRT.

Megoldás. Legyen $\displaystyle AP=AQ=x$ és $\displaystyle BR=y$. Feltehető, hogy $\displaystyle P$ az $\displaystyle AB$ él belső pontja, azaz $\displaystyle 0<x<1$, különben $\displaystyle P=Q$ vagy $\displaystyle P=R$, és a $\displaystyle QPR\angle$ nem jön létre.

A Pitagorasz-tétel többszöri alkalmazásával kapjuk, hogy $\displaystyle PQ^2=AQ^2+AP^2=2x^2$, $\displaystyle PR^2=BP^2+BR^2=(1-x)^2+y^2$ és $\displaystyle QR^2=AQ^2+AB^2+BR^2=x^2+y^2+1$.

Írjuk fel a koszinusz-tételt a $\displaystyle PQR$ háromszögben a $\displaystyle P\angle$-re: $\displaystyle QR^2=PQ^2+PR^2-2 \cdot PQ\cdot PR \cdot \cos 120^\circ$. Ebbe beírva a fentieket kapjuk, hogy

$\displaystyle x^2+y^2+1=2x^2+(1-x)^2+y^2-2\cdot \sqrt{2x^2} \cdot \sqrt{(1-x)^2+y^2}\cdot \frac {-1}2.$

Rendezés majd négyzetreemelés után:

$\displaystyle (-2x^2+2x)^2=(2x^2)\cdot ((1-x)^2+y^2).$

Kihasználva, hogy $\displaystyle x>0$, oszhatunk $\displaystyle 2x^2$-tel, így kapjuk, hogy $\displaystyle 2(x-1)^2=(x-1)^2+y^2$, azaz $\displaystyle y^2=(x-1)^2$. Ebből $\displaystyle x< 1$ és $\displaystyle y>0$ miatt $\displaystyle y=1-x$ következik, azaz a $\displaystyle BR$ távolság $\displaystyle 1-x$.

Statisztika:

106 dolgozat érkezett.
4 pontot kapott:	84 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2020. szeptemberi matematika feladatai