A B. 5200. feladat (2021. november)

B. 5200. Az $\displaystyle A_0A_1=1$ átmérőjű félkörvonalon felvesszük az $\displaystyle A_2$ pontot úgy, hogy $\displaystyle A_0A_1A_2\sphericalangle=1^\circ$. Ezután a körvonal $\displaystyle A_1A_2$ ívén felvesszük az $\displaystyle A_3$ pontot úgy, hogy $\displaystyle A_1A_2A_3\sphericalangle=2^\circ$. Ezt folytatjuk a következők szerint: az $\displaystyle A_{k+1}$ pontot a körvonal $\displaystyle A_{k-1}A_k$ ívén választjuk úgy, hogy $\displaystyle A_{k-1}A_kA_{k+1}$ szög $\displaystyle k$ fok ($\displaystyle k=3,4,\ldots,9$). Milyen hosszú az $\displaystyle A_9A_{10}$ szakasz? (Az ábra tájékoztató jellegű.)

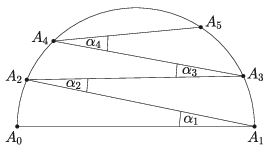
(3 pont)

A beküldési határidő 2021. december 10-én LEJÁRT.

Megoldás. Kössük össze az $\displaystyle A_i$ pontokat a félkörvonal $\displaystyle O$ középpontjával, és vezessük be az $\displaystyle OA_iA_{i+1}\angle=\beta_i$ jelölést. Világos, hogy $\displaystyle \beta_1=1^\circ$. Továbbá mivel az $\displaystyle OA_iA_{i+1}\triangle$ egyenlő szárú, így

$\displaystyle \beta_{i+1}=OA_{i+1}A_{i+2}\angle=OA_{i+1}A_{i}\angle+A_iA_{i+1}A_{i+2}\angle=\beta_i+(i+1)^\circ\qquad (i=1,2,\ldots,8).$

Ezt nyolcszor alkalmazva $\displaystyle \beta_9=45^\circ$, tehát $\displaystyle OA_9A_{10}$ derékszögű egyenlő szárú háromszög. Végül Pitagorasz-tétellel $\displaystyle A_9A_{10}=\sqrt{(1/2)^2+(1/2)^2}=\sqrt 2/2$ adódik.

Statisztika:

108 dolgozat érkezett.
3 pontot kapott:	76 versenyző.
2 pontot kapott:	21 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2021. novemberi matematika feladatai