 |
A B. 5270. feladat (2022. november) |
B. 5270. n2 darab egységnyi oldalú szabályos háromszögből egy n egység oldalú háromszöget állítottunk össze, és a kis háromszögeket felváltva sötétre és világosra színeztük. A háromszögekbe beírtuk sorban az 1,2,3,…,n2 számokat az ábra szerint. Mennyi a sötét háromszögekbe írt számok összege?
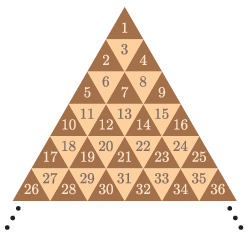
Javasolta: Németh László (Fonyód)
(3 pont)
A beküldési határidő 2022. december 12-én LEJÁRT.
Megoldás. Felülről a k-adik ,,sorban'' a háromszögek száma 2k−1, így az első k sorban összesen annyi háromszög van, mint az első k pozitív páratlan szám összege, vagyis k2. Tehát a k-adik sorban lévő háromszögekbe írt számok:
(k−1)2+1,(k−1)2+2,…,k2.
Az első és az utolsó háromszög mindig sötét, így a k-adik sorban lévő sötét háromszögekbe írt számok egy k hosszúságú számtani sorozatot alkotnak, összegük
((k−1)2+1)+((k−1)2+3)+⋯+k2=((k−1)2+1)+k22⋅k=k3−k2+k.
A sötét háromszögekbe írt számok összege így
n∑k=1(k3−k2+k)=n∑k=1k3−n∑k=1k2+n∑k=1k==n2(n+1)24−n(n+1)(2n+1)6+n(n+1)2=n(n+1)(3n2−n+4)12.Tehát a sötét háromszögekbe írt számok összege
n(n+1)(3n2−n+4)12.
Statisztika:
163 dolgozat érkezett. 3 pontot kapott: 109 versenyző. 2 pontot kapott: 21 versenyző. 1 pontot kapott: 19 versenyző. 0 pontot kapott: 7 versenyző. Nem versenyszerű: 2 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2022. novemberi matematika feladatai
|
|

