A B. 5325. feladat (2023. május)

B. 5325. Adjuk meg az összes olyan korlátos, konvex poliédert, amelynek lapsíkjai \(\displaystyle c+e+\ell+1\) részre bontják a teret, ahol \(\displaystyle c\), \(\displaystyle e\) és \(\displaystyle \ell\) rendre a poliéder csúcsainak, éleinek és lapjainak számát jelöli.

Javasolta: Vígh Viktor (Sándorfalva)

(6 pont)

A beküldési határidő 2023. június 12-én LEJÁRT.

Megoldás. Először egy ismert állítást elevenítünk fel.

Tétel. \(\displaystyle n\) általános helyzetű egyenes a síkot \(\displaystyle {n \choose 0}+{n\choose 1}+{n \choose 2}=(n^2+n+2)/2\) darabra bontja.

Bizonyítás. Jelölje az adott egyeneseket \(\displaystyle e_1\), \(\displaystyle e_2\), \(\displaystyle \ldots\), \(\displaystyle e_n\). Mivel az egyenesek általános helyzetűek, így bármely kettő metszi egymást, és semelyik három nem illeszkedik közös pontra. Így metszéspontjaik száma \(\displaystyle k=n(n-1)/2\). Legyenek a metszéspontok \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\). Tekinsünk egy \(\displaystyle \ell\) egyenest, ami nem párhuzamos a \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\) által meghatározott egyenesek egyikével sem, valamint a \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\) pontok mind \(\displaystyle \ell\) ugyanazon oldalára esnek. (Egy ponthalmaz meghatároz egy egyenest, ha a ponthalmaz legalább két pontja illeszkedik az egyenesre.)

Az \(\displaystyle \ell\) egyenes az \(\displaystyle e_1\), \(\displaystyle e_2\), \(\displaystyle \ldots\), \(\displaystyle e_n\) egyenesek mindegyikét egy-egy pontban metszi. Ha az \(\displaystyle \ell\) egyenesen ,,végigsétálunk'', pontosan akkor lépünk át egy síkrészből egy másikba, amikor áthaladunk egy ilyen metszésponton, így az \(\displaystyle \ell\) egyenes pontosan \(\displaystyle n+1\) létrejött síkrészt metsz.

Most képzeletben seperjünk végig az \(\displaystyle \ell\) egyenessel a \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\) pontokon, vagyis toljuk el párhuzamosan \(\displaystyle \ell\)-t folytonosan addig, míg az összes \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\) pont át nem kerül \(\displaystyle \ell\) másik oldalára. Az \(\displaystyle \ell\) speciális választása miatt a \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle \ldots\), \(\displaystyle P_k\) pontokon egyesével ,,haladunk át''. Egy ábrával könnyen meggyőződhetünk róla, hogy minden egyes ilyen áthaladáskor \(\displaystyle \ell\) elhagy egy korábban metszett síkrészt, és helyette egy új síkrészbe metsz bele.

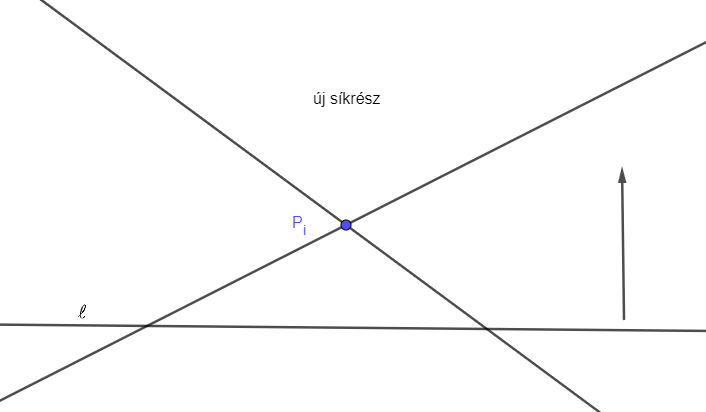
A leírtakból következik, hogy a létrejött síkrészek száma megegyezik a kezdetben metszett síkrészek számának és a metszéspontok számának összegével, vagyis \(\displaystyle (n+1)+n(n-1)/2=(n^2+n+2)/2\), ahogy állítottuk. \(\displaystyle \square\)

A fenti módszer a térben is működik, és hasonló megfontolással kapjuk, hogy \(\displaystyle n\) általános helyzetű sík a teret pontosan \(\displaystyle {n \choose 0}+{n\choose 1}+{n \choose 2}+{n \choose 3}\) részre vágja. Ennek az állításnak egy változatára lesz szükségünk:

Állítás. Adott a térben \(\displaystyle n\) különböző sík, amelyek összesen \(\displaystyle m\) egyenesben és \(\displaystyle p\) pontban metszik egymást. (Pontosan \(\displaystyle m\) olyan egyenes van, amelyik legalább két síkra illeszkedik, és pontosan \(\displaystyle p\) olyan pont van, amelyik legalább három síkra illeszkedik.) Ekkor a síkok a teret legalább \(\displaystyle n+m+p+1\) részre bontják.

Bizonyítás. Legyenek az adott síkok \(\displaystyle S_1, \ldots, S_n\), a metszetegyenesek \(\displaystyle f_1, \ldots, f_m\), és a metszéspontok \(\displaystyle Q_1, \ldots, Q_p\). Válasszunk egy \(\displaystyle S\) síkot, amely sem az \(\displaystyle e_i\) metszésegyenesek, sem a \(\displaystyle P_i\) metszéspontok által meghatározott egyenesek egyikével sem párhuzamos, és a \(\displaystyle P_i\) metszéspontok mind a sík egyik oldalára esnek.

Jelölje \(\displaystyle e_i\) az \(\displaystyle S\cap S_i\) metszetegyeneseket. Vegyük észre, hogy minden \(\displaystyle P_i=S\cap f_i\) metszéspont egyúttal néhány (legalább kettő) \(\displaystyle e_i\) egyenes metszéspontja is. Megbecsüljük, hogy az \(\displaystyle e_i\) egyenesek hány részre osztják az \(\displaystyle S\) síkot. Ehhez – az első tétel bizonyításához hasonlóan – válasszunk egy seprőegyenest az \(\displaystyle S\) síkon. Ez kezdetben \(\displaystyle n+1\) síkrészt metsz, mivel minden \(\displaystyle e_i\) egyenes metszi. Amikor egy metszésponton áttoljuk a seprőegyeneset, akkor legalább egy új síkrészbe fog belemetszeni. Így az \(\displaystyle e_i\) egyesek az \(\displaystyle S\) síkot legalább \(\displaystyle n+1+m\) részre bontják (mivel legalább \(\displaystyle m\) metszéspontunk van). Ebből következően az \(\displaystyle S\) sík legalább \(\displaystyle n+m+1\) térrészt metsz, amelyet az \(\displaystyle S_i\) síkok hoztak létre.

Most, hasonlóan az előzőekhez, seperjünk végig az \(\displaystyle S\) síkkal a téren úgy, hogy a \(\displaystyle Q_i\) metszéspontok mind a másik oldalára kerüljenek. Hasonlóan a síkhoz, minden ponton történő áthaladáskor legalább egy új térrészbe metsz bele \(\displaystyle S\). Mivel kezdetben legalább \(\displaystyle n+m+1\) térrészbe metszett bele, majd mind a \(\displaystyle p\) darab pontnál legalább egy újabba, így összesen legalább \(\displaystyle n+m+p+1\) részre bontják az \(\displaystyle S_i\) síkok a teret, ahogy állítottuk. \(\displaystyle \square\)

Tekintsünk most egy korlátos poliédert, amelynek lapsíkjai \(\displaystyle S_1, \ldots, S_\ell\), és a poliédernek \(\displaystyle e\) darab éle és \(\displaystyle c\) darab csúcsa van. Világos, hogy ekkor az \(\displaystyle S_i\) lapsíkok legalább \(\displaystyle e\) darab egyenesben és legalább \(\displaystyle c\) darab pontban metszik egymást, ezért az állításunk szerint a lapsíkok a teret legalább \(\displaystyle c+e+\ell+1\) részre bontják. Továbbá, ha a lapsíkoknak van az élegyeneseken kívül további metszetegyenesük, vagy a csúcsokon kívül további metszéspontjuk, akkor már több, mint \(\displaystyle c+e+\ell+1\) részre bontják a lapsíkok a teret, azaz a feladat feltétele nem teljesülhet.

Azt kaptuk tehát, hogy a feltételeknek megfelelő poliéder bármely két lapsíkja szükségképpen élegyenesben metszi egymást, azaz bármely két lap vagy szomszédos, vagy párhuzamos. Tekintsünk most egy tetszőleges \(\displaystyle F\) lapot, és a vele szomszédos \(\displaystyle F_1, \ldots, F_k\) lapokat. Világos, hogy \(\displaystyle F_1\) az \(\displaystyle F_2, \ldots, F_k\) lapok közül legfeljebb kettővel szomszédos, és legfeljebb további eggyel párhuzamos, azaz \(\displaystyle k\leq 4\). Ezen észrevételből azonnal következik, hogy a keresett poliédernek legfeljebb hat lapja lehet, és az eseteket végignézve a következő lehetőségeket kapjuk: tetraéder, háromszög alapú (ferde) hasáb és paralelepipedon. Megmutatjuk, hogy ezek mind megfelelőek.

A tetraéder lapsíkjai általános helyzetűek, így ezekre érvényes az általános tételünk, azaz a lapsíkok a teret valóban \(\displaystyle 4+6+4+1=15\) részre bontják.

A háromszög alapú hasáb és a paralelepipedon esetén válasszunk egy párhuzamos lappárt (ilyen mindkettő esetben van). Ezek a teret három rétegre bontják. Egy-egy rétegben pontosan annyi térrész van, ahány részre egy háromszög ill. paralelogramma oldalegyenesei bontják a síkot, azaz \(\displaystyle 7\) ill. \(\displaystyle 9\). Ebből következően a háromszög alapú hasáb lapsíkjai \(\displaystyle 3\cdot 7=21\) részre bontják a teret, míg a paralelepipedon lapsíkjai \(\displaystyle 3\cdot 9=27\) részre. Mivel a háromszög alapú hasábnak \(\displaystyle 6\) csúcsa, \(\displaystyle 9\) éle és \(\displaystyle 5\) lapja van, és \(\displaystyle 6+9+5+1=21\), így ez valóban megfelelő. Hasonlóan, a paralelepipedonnak \(\displaystyle 8\) csúcsa, \(\displaystyle 12\) éle és \(\displaystyle 6\) lapja van, és \(\displaystyle 8+12+6+1=27\), szintén megfelelő.

Összességében kaptuk, hogy a keresett poliéderek a tetraéderek, a háromszög alapú (ferde) hasábok és a paralelepipedonok.

Statisztika:

20 dolgozat érkezett.
6 pontot kapott:	Chrobák Gergő, Czirják Márton Pál, Diaconescu Tashi, Hodossy Réka, Holló Martin, Kocsis 827 Péter, Kovács Benedek Noel, Melján Dávid Gergő, Prohászka Bulcsú, Szakács Ábel, Szalontai Júlia, Varga Boldizsár, Veres Dorottya, Vigh 279 Zalán.
5 pontot kapott:	Bodor Mátyás.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. májusi matematika feladatai