A B. 5374. feladat (2024. március)

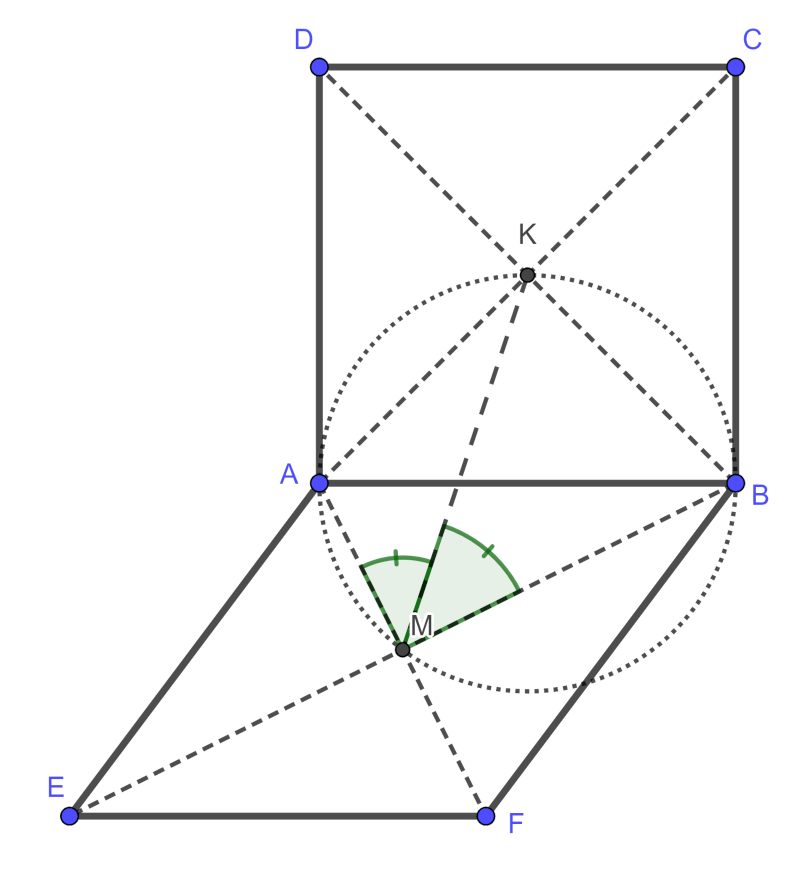
B. 5374. Az \(\displaystyle AB\) szakasz egyik oldalára megrajzoltuk az \(\displaystyle ABCD\) négyzetet, a másik oldalára pedig a \(\displaystyle BAEF\) rombuszt. A négyzet középpontja legyen \(\displaystyle K\), a rombuszé \(\displaystyle M\). Bizonyítsuk be, hogy \(\displaystyle KM\) felezi az \(\displaystyle AMB\) szöget.

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

A beküldési határidő 2024. április 10-én LEJÁRT.

Megoldás. Minden rombuszra (és így minden négyzetre) teljesül, hogy átlói merőlegesek, tehát \(\displaystyle BKA \sphericalangle = AMB \sphericalangle = 90^{\circ}\). Ekkor \(\displaystyle K\) és \(\displaystyle M\) is rajta van az \(\displaystyle AB\) szakasz Thalész-körén. \(\displaystyle AK = KB\) (hiszen egy négyzet átlói egyenlő hosszúak és felezik egymást), tehát a kerületi szögek tétele miatt \(\displaystyle BMK \sphericalangle = KMA \sphericalangle\) – éppen ezt kellett bizonyítanunk.

Statisztika:

114 dolgozat érkezett.
3 pontot kapott:	93 versenyző.
2 pontot kapott:	13 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	4 dolgozat.

A KöMaL 2024. márciusi matematika feladatai