 |
A B. 5381. feladat (2024. március) |
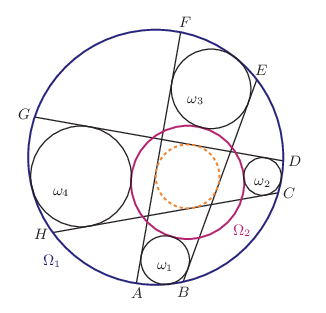
B. 5381. Adott az \(\displaystyle \Omega_1\) körbe írt \(\displaystyle ABCDEFGH\) nyolcszög, és \(\displaystyle \Omega_1\) belsejében az \(\displaystyle \Omega_2\) kör. Tegyük fel, hogy az \(\displaystyle \omega_1\), \(\displaystyle \omega_2\), \(\displaystyle \omega_3\), \(\displaystyle \omega_4\) körök kívülről érintik \(\displaystyle \Omega_2\)-t, továbbá \(\displaystyle \omega_1\) belülről érinti az \(\displaystyle \Omega_1\) kör \(\displaystyle AB\) ívét, az \(\displaystyle AF\) és a \(\displaystyle BE\) szakaszt; \(\displaystyle \omega_2\) belülről érinti a \(\displaystyle CD\) ívet, a \(\displaystyle CH\) és a \(\displaystyle DG\) szakaszt; \(\displaystyle \omega_3\) belülről érinti az \(\displaystyle EF\) ívet, az \(\displaystyle AF\) és a \(\displaystyle BE\) szakaszt; végül \(\displaystyle \omega_4\) belülről érinti a \(\displaystyle GH\) ívet, a \(\displaystyle CH\) és a \(\displaystyle DG\) szakaszt az ábra szerint. Mutassuk meg, hogy az \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) szakaszok által bezárt négyszögbe kört lehet írni.
Javasolta: Kós Géza (Budapest)
(6 pont)
A beküldési határidő 2024. április 10-én LEJÁRT.
Megoldás. Térbe kilépéssel, a körökre illesztett kúpokkal bizonyítunk.
Az \(\displaystyle AF\) egyenesnek a \(\displaystyle B\), \(\displaystyle E\) pontokat tartalmazó oldalát az egyenes belső oldalának fogjuk hívni, és ugyanígy, a \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyeneseknek az \(\displaystyle A\), \(\displaystyle F\), a \(\displaystyle D\), \(\displaystyle G\), illetve \(\displaystyle C\), \(\displaystyle H\) pontokat tartalmazó oldalát is az illető egyenes belső oldalának nevezzük. A feladatunk egy olyan kör megszerkesztése, amely az \(\displaystyle AF\), a \(\displaystyle BE\), a \(\displaystyle CH\) és a \(\displaystyle DG\) egyenest is a belső oldalán érinti.
Az ábra síkját – a továbbiakban alapksíknak fogjuk hívni – helyezzük el a térben. A sík egyik oldalára mondjuk azt, hogy a sík fölött van. Például, az alapsík lehet a térbeli derékszögű koordináta-rendszer \(\displaystyle x\)–\(\displaystyle y\) síkja, az alapsík fölötti pontok a pozitív \(\displaystyle z\)-koordinátájú pontok. Az alapsíkban fekvő köröket feleltessük meg az alapsík fölötti féltér pontjainak a következőképpen. Ha \(\displaystyle k\) tetszőleges kör a síkban, akkor illesszünk rá egy \(\displaystyle 45^\circ\)-os meredekségű kúpot; a kúp csúcsát jelöljük \(\displaystyle V(k)\)-val. Másképpen fogalmazva, ha \(\displaystyle k\) az \(\displaystyle (x,y)\) középpontú, \(\displaystyle r\) sugarú kör, akkor legyen \(\displaystyle V(k)=(x,y,r)\). Megfordítva, minden, a sík fölötti \(\displaystyle P=(x,y,r)\) ponthoz létezik egy \(\displaystyle 45^\circ\)-os meredekségű kúp, amelynek csúcsa \(\displaystyle V\), és alapköre az alapsíkban van, nevezetesen az \(\displaystyle (x,y)\) középpontú, \(\displaystyle r\) sugarú kör; jelöljük ezt a kört \(\displaystyle \kappa(P)\)-vel.
Szükségünk lesz a következő egyszerű észrevételre. Tegyük fel, hogy az alapsíkban adott egy \(\displaystyle \ell\) határú \(\displaystyle \mathcal{F}\) félsík, és vizsgáljuk azokat a \(\displaystyle k\) köröket, amelyek \(\displaystyle \mathcal{F}\)-ben fekszenek, és érintik \(\displaystyle \ell\)-et. Látható, hogy az összes ilyen körökhöz tartozó \(\displaystyle V(k)\) pontok halmaza egy félsík, ami illeszkedik \(\displaystyle \ell\)-re, az \(\displaystyle \mathcal{F}\)-fel \(\displaystyle 45^\circ\)-os szöget zár be, és persze az alapsík felső oldalán van.
Tekintsük az alapsíkban azokat a \(\displaystyle k\) köröket, amelyek az \(\displaystyle AF\) egyenest a belső oldalán érintik. A fenti észrevétel szerint a \(\displaystyle V(k)\) pontok egy \(\displaystyle AF\)-re illeszkedő \(\displaystyle \mathcal{F}_{AF}\) félsíkban vannak. Hasonlóan, a \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyeneseket a belső oldalukon érintő körökhöz rendelt csúcsok is egy-egy, az illető egyenesre illesztett félsík, \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), illetve \(\displaystyle \mathcal{F}_{DG}\) pontjai. A feladat megoldásához azt kell igazolnunk, hogy az \(\displaystyle \mathcal{F}_{AF}\), \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), \(\displaystyle \mathcal{F}_{DG}\) félsíkoknak van egy közös \(\displaystyle W\) pontja.
Legyen \(\displaystyle V_1=V(\omega_1)\), \(\displaystyle V_2=V(\omega_2)\), \(\displaystyle V_3=V(\omega_3)\), illetve \(\displaystyle V_4=V(\omega_4)\). Mivel \(\displaystyle \omega_1\) és \(\displaystyle \omega_3\) a belső oldalon érinti az \(\displaystyle AF\) és a \(\displaystyle BE\) egyenest, az \(\displaystyle \mathcal{F}_{AF}\) és \(\displaystyle \mathcal{F}_{BE}\) félsíkoknak \(\displaystyle V_1\) és \(\displaystyle V_3\) is közös pontja, ezért mindkét félsík tartalmazza a \(\displaystyle V_1V_3\) szakaszt. Hasonlóan, az \(\displaystyle \mathcal{F}_{CH}\) és a \(\displaystyle \mathcal{F}_{DG}\) félsík is tartalmazza a \(\displaystyle V_2V_4\) szakaszt.
Most megmutatjuk, hogy a \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok egy síkban fekszenek. Illesszük az \(\displaystyle \Omega_1\) körre a \(\displaystyle \mathcal{G}_1\), az \(\displaystyle \Omega_2\)-re a \(\displaystyle \mathcal{G}_2\) gömböt úgy, hogy ezek \(\displaystyle 45^\circ\)-os szögben messék az alapsíkot, \(\displaystyle \mathcal{G}_1\) középpontja az alapsík fölött, \(\displaystyle \mathcal{G}_2\) középpontja a sík alatt legyen. Legyen \(\displaystyle \omega_i\) és \(\displaystyle \Omega_1\) érintési pontja \(\displaystyle T_i\), az \(\displaystyle \omega_i\) és \(\displaystyle \Omega_2\) érintési pontja pedig \(\displaystyle U_i\). Az \(\displaystyle \omega_i\)-re emelt kúp \(\displaystyle V_iT_i\) alkotója érinti \(\displaystyle \mathcal{G}_1\)-et, míg ugyanennek a kúpnak a \(\displaystyle V_iU_i\) alkotója érinti \(\displaystyle \mathcal{G}_2\)-t. A \(\displaystyle V_i\) csúcsból tehát ugyanolyan hosszú érintőt lehet húzni a két gömbhöz, tehát mindegyik \(\displaystyle V_i\) csúcs a két gömb hatványsíkjában van.
A \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok merőleges vetülete az ábra síkjára az \(\displaystyle AF\) és a \(\displaystyle BE\), illetve a \(\displaystyle CH\) és \(\displaystyle DG\) egyenesek középvonalai, ezek metszik az \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyenesek által meghatározott négyszög odalait, és a négyszög belsejében metszik egymást. Ezért az (egy síkban fekvő) \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok is metszik egymást a térben. Legyen \(\displaystyle W\) a két szakasz metszéspontja; ekkor tehát \(\displaystyle W\) közös pontja az \(\displaystyle \mathcal{F}_{AF}\), \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), \(\displaystyle \mathcal{F}_{DG}\) félsíkoknak, vagyis a \(\displaystyle \kappa(W)\) kör a belső oldalán érinti az \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\), \(\displaystyle DG\) egyeneseket.
Statisztika:
3 dolgozat érkezett. 6 pontot kapott: Bodor Mátyás, Forrai Boldizsár, Virág Tóbiás.
A KöMaL 2024. márciusi matematika feladatai