A B. 5387. feladat (2024. április)

B. 5387. A sík véges sok pontját megjelöltük a piros, kék és zöld színek valamelyikével úgy, hogy nincs három kollineáris, azonos színű pont, de bármely két azonos színű pontot összekötő szakaszon van olyan megjelölt pont, amelynek színe különbözik a végpontok színétől. Legfeljebb hány pontot vehettünk fel?

Javasolta: Róka Sándor (Nyíregyháza)

(5 pont)

A beküldési határidő 2024. május 10-én LEJÁRT.

Megoldás. Megmutatjuk, hogy a pontok száma legfeljebb 6. Ha lenne legalább 7 pont, azok között volna három azonos színű. Három azonos színű pont nem eshet egy egyenesre, hiszen akkor a két szélsőt összekötő szakaszon lenne velük megegyező színű pont. Tehát bármely három azonos színű pont valódi (pozitív területű) háromszöget alkot.

Az azonos színű ponthármasok közül válasszunk egy minimális területűt. Legyen ez egy kék háromszög. (Lásd a bal oldalon lévő ábrát.) A háromszög mindegyik oldalán van (legalább) egy-egy pont, amely piros vagy zöld színű. Ez a három pont nem lehet egyszínű, mert akkor az általuk alkotott egyszínű háromszög területe kisebb lenne a kiválasztott háromszög területénél. Az oldalakon lévő pontok közül kettő azonos színű (legyen piros), a harmadik zöld.

A két piros pontot összekötő szakaszon is kell legyen (legalább) egy kék vagy zöld pont. Ha kék lenne, akkor a háromszög bármely két csúcsával egy a minimálisnál kisebb területű kék háromszöget adna. Tehát ez a pont zöld.

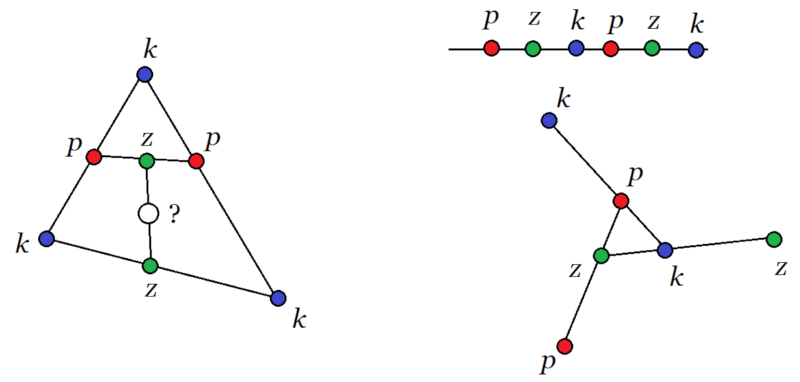
A két zöld pontunkat összekötő szakaszon is kell hogy legyen egy piros vagy kék pont. Ez azonban nem lehet kék, és nem lehet piros sem, mert akkor ismét találunk egy, a kiválasztott háromszögnél kisebb területű egyszínű háromszöget. Ellentmondásra jutottunk abból a feltevésből kiindulva, hogy a pontrendszer legalább 7 pontból áll. Tehát legfeljebb 6 pontunk lehet, és van is ilyen pontrendszer. A jobb oldalon lévő ábrák két különböző lehetséges elrendezést mutatnak.

Statisztika:

66 dolgozat érkezett.
5 pontot kapott:	Ali Richárd, Baran Júlia, Bencze Mátyás, Bodor Mátyás, Bővíz Dániel, Christ Miranda Anna, Csató Hanna Zita , Csonka Illés, Csupor Albert Dezső, Danka Emma, Diaconescu Tashi, Farkas 005 Bendegúz, Fórizs Emma, Gömze Norken, Gyenes Károly, Hodossy Réka, Holló Martin, Keresztély Zsófia, Kovács Benedek Noel, Morvai Várkony Albert, Németh Bernát, Op Den Kelder Ábel, Pálfi András, Petrányi Lilla, Pletikoszity Martin, Prohászka Bulcsú, Sági Mihály, Sánta Gergely Péter, Sárdinecz Dóra, Sütő Áron, Szabó 721 Sámuel, Tamás Gellért, Varga 511 Vivien, Virág Lénárd Dániel, Wágner Márton.
4 pontot kapott:	Balassa János, Deák Boldizsár Tamás, Forrai Boldizsár, Földi Krizsán Kitty, Illés Dóra, Klement Tamás, Kővágó Edit Gréta, Maróti Bálint, Miszori Gergő, Pázmándi József Áron, Tulkán Dávid, Vigh 279 Zalán, Virág Tóbiás, Zhai Yu Fan.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2024. áprilisi matematika feladatai