Problem B. 5389. (April 2024)

B. 5389. Let \(\displaystyle I\) denote the incenter of acute triangle \(\displaystyle ABC\). Let the incircle touch sides \(\displaystyle BC\) and \(\displaystyle AC\) at points \(\displaystyle D\) and \(\displaystyle E\), respectively. Let \(\displaystyle H\) denote the orthocenter of triangle \(\displaystyle ABC\). Prove that if \(\displaystyle H\) is on line segment \(\displaystyle DE\), then line \(\displaystyle HI\) bisects side \(\displaystyle AB\).

Proposed by Boldizsár Varga, Budapest

(6 pont)

Deadline expired on May 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit, legyen \(\displaystyle H\) tükörképe az \(\displaystyle AB\) oldal \(\displaystyle F\) felezőpontjára \(\displaystyle C'\). Jól ismert (lásd pl. Horvay-Reiman: Geometriai feladatok gyűjteménye I., 1081. feladat), hogy \(\displaystyle C'\) éppen az \(\displaystyle ABC\) körülírt kör \(\displaystyle C\)-vel átellenes pontja.

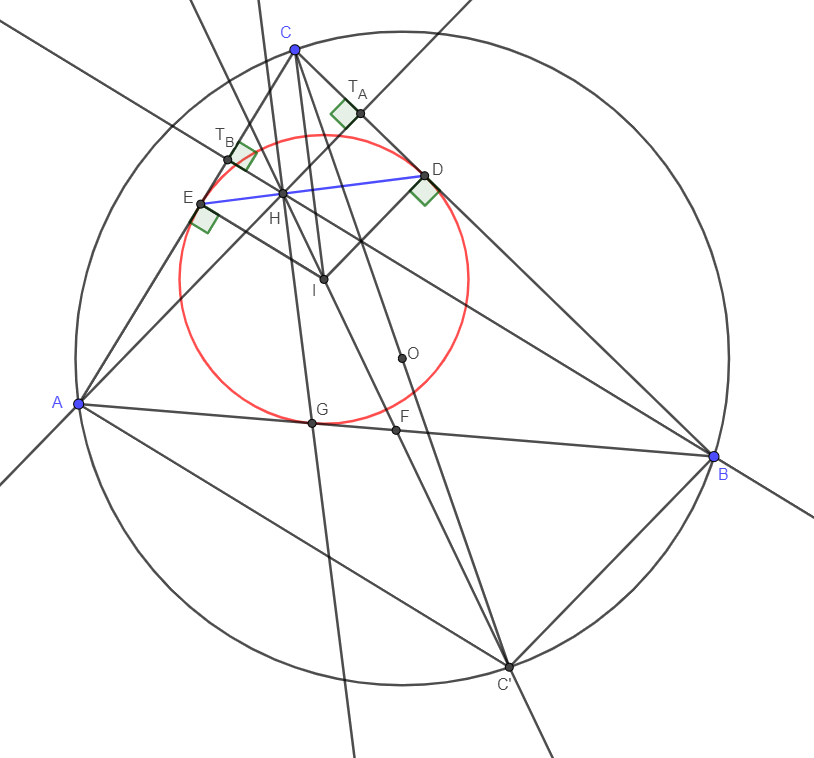
Thalész tétele miatt \(\displaystyle C'A\) merőleges az \(\displaystyle AC\) oldalra, s így \(\displaystyle AC'\parallel EI\parallel T_BH\), hiszen mindhárom egyenes merőleges \(\displaystyle AC\)-re. (\(\displaystyle T_B\) a \(\displaystyle B\)-ből induló magasság talppontja.) Hasonlóan belátható, hogy \(\displaystyle BC'\parallel DI\parallel T_AH\).

A \(\displaystyle C\)-nél lévő szöget \(\displaystyle \gamma\)-val jelölve \(\displaystyle T_AAC\sphericalangle=90^\circ -\gamma=T_BBC\sphericalangle\) miatt a \(\displaystyle HAT_B\triangle\) és \(\displaystyle HBT_A\triangle\) derékszögű háromszögek egyik hegyesszöge megyegyezik, ezért \(\displaystyle HAT_B\triangle \sim HBT_A\triangle\).

Vegyük észre, hogy \(\displaystyle CD=CE\), hiszen külső pontból körhöz húzott érintőszakaszok egyenlőek, így \(\displaystyle CED\triangle\) egyenlő szárú, és \(\displaystyle CED\sphericalangle=CDE\sphericalangle\). Így a \(\displaystyle T_BEH\triangle\) és \(\displaystyle T_ADH\triangle\) derékszögű háromszögek egyik hegyesszöge egyenlő, ezért \(\displaystyle T_BEH\triangle\sim T_ADH\triangle\). A két igazolt hasonlóságot felhasználva

\(\displaystyle \frac{T_BE}{T_BA}=\frac{\frac{T_BE}{T_BH}}{\frac{T_BA}{T_BH}}=\frac{\frac{T_AD}{T_AH}}{\frac{T_AB}{T_AH}}=\frac{T_AD}{T_AB},\)

amiből \(\displaystyle AE:ET_B=BD:DT_A\), azaz \(\displaystyle D\) ugyanolyan arányban osztja \(\displaystyle BT_A\)-t, mint \(\displaystyle E\) osztja \(\displaystyle AT_B\)-t.

Most messük az \(\displaystyle AT_B\) és \(\displaystyle HC'\) egyenesek által adott szög szárait a párhuzamos \(\displaystyle T_BH\), \(\displaystyle EI\) és \(\displaystyle AC'\) egyenesekkel; valamint a \(\displaystyle HC'\) és \(\displaystyle T_AB\) egyenesek által adott szög szárait a párhuzamos \(\displaystyle T_AH\), \(\displaystyle DI\) és \(\displaystyle BC'\) egyenesekkel. Az előbb igazolt arányok egyenlősége, és a párhuzamos szelők tétele miatt az \(\displaystyle EI\) és \(\displaystyle DI\) egyenesek \(\displaystyle HC'\)-n metszik egymást, azaz az \(\displaystyle I\) pont illeszkedik \(\displaystyle HC'\)-re, amiből az állítás következik.

Statistics:

15 students sent a solution.
6 points:	Ali Richárd, Bodor Mátyás, Csonka Illés, Diaconescu Tashi, Gömze Norken, Holló Martin, Keresztély Zsófia, Kovács Benedek Noel, Romaniuc Albert-Iulian, Vigh 279 Zalán.
5 points:	Forrai Boldizsár, Jármai Roland.
2 points:	2 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, April 2024