A B. 5389. feladat (2024. április)

B. 5389. Az \(\displaystyle ABC\) hegyesszögű háromszög beírt körének középpontja \(\displaystyle I\), a \(\displaystyle BC\) és \(\displaystyle AC\) oldalakkal vett érintési pontjai \(\displaystyle D\), illetve \(\displaystyle E\), továbbá jelölje \(\displaystyle H\) a háromszög magasságpontját. Igazoljuk, hogy ha \(\displaystyle H\) a \(\displaystyle DE\) szakaszon van, akkor a \(\displaystyle HI\) egyenes felezi az \(\displaystyle AB\) oldalt.

Javasolta: Varga Boldizsár (Budapest)

(6 pont)

A beküldési határidő 2024. május 10-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit, legyen \(\displaystyle H\) tükörképe az \(\displaystyle AB\) oldal \(\displaystyle F\) felezőpontjára \(\displaystyle C'\). Jól ismert (lásd pl. Horvay-Reiman: Geometriai feladatok gyűjteménye I., 1081. feladat), hogy \(\displaystyle C'\) éppen az \(\displaystyle ABC\) körülírt kör \(\displaystyle C\)-vel átellenes pontja.

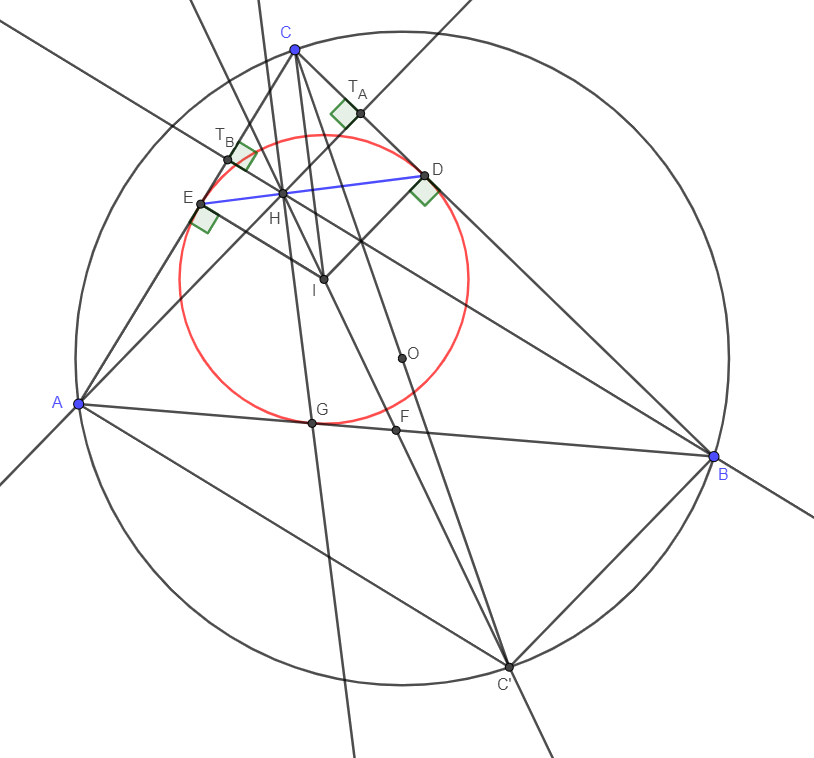
Thalész tétele miatt \(\displaystyle C'A\) merőleges az \(\displaystyle AC\) oldalra, s így \(\displaystyle AC'\parallel EI\parallel T_BH\), hiszen mindhárom egyenes merőleges \(\displaystyle AC\)-re. (\(\displaystyle T_B\) a \(\displaystyle B\)-ből induló magasság talppontja.) Hasonlóan belátható, hogy \(\displaystyle BC'\parallel DI\parallel T_AH\).

A \(\displaystyle C\)-nél lévő szöget \(\displaystyle \gamma\)-val jelölve \(\displaystyle T_AAC\sphericalangle=90^\circ -\gamma=T_BBC\sphericalangle\) miatt a \(\displaystyle HAT_B\triangle\) és \(\displaystyle HBT_A\triangle\) derékszögű háromszögek egyik hegyesszöge megyegyezik, ezért \(\displaystyle HAT_B\triangle \sim HBT_A\triangle\).

Vegyük észre, hogy \(\displaystyle CD=CE\), hiszen külső pontból körhöz húzott érintőszakaszok egyenlőek, így \(\displaystyle CED\triangle\) egyenlő szárú, és \(\displaystyle CED\sphericalangle=CDE\sphericalangle\). Így a \(\displaystyle T_BEH\triangle\) és \(\displaystyle T_ADH\triangle\) derékszögű háromszögek egyik hegyesszöge egyenlő, ezért \(\displaystyle T_BEH\triangle\sim T_ADH\triangle\). A két igazolt hasonlóságot felhasználva

\(\displaystyle \frac{T_BE}{T_BA}=\frac{\frac{T_BE}{T_BH}}{\frac{T_BA}{T_BH}}=\frac{\frac{T_AD}{T_AH}}{\frac{T_AB}{T_AH}}=\frac{T_AD}{T_AB},\)

amiből \(\displaystyle AE:ET_B=BD:DT_A\), azaz \(\displaystyle D\) ugyanolyan arányban osztja \(\displaystyle BT_A\)-t, mint \(\displaystyle E\) osztja \(\displaystyle AT_B\)-t.

Most messük az \(\displaystyle AT_B\) és \(\displaystyle HC'\) egyenesek által adott szög szárait a párhuzamos \(\displaystyle T_BH\), \(\displaystyle EI\) és \(\displaystyle AC'\) egyenesekkel; valamint a \(\displaystyle HC'\) és \(\displaystyle T_AB\) egyenesek által adott szög szárait a párhuzamos \(\displaystyle T_AH\), \(\displaystyle DI\) és \(\displaystyle BC'\) egyenesekkel. Az előbb igazolt arányok egyenlősége, és a párhuzamos szelők tétele miatt az \(\displaystyle EI\) és \(\displaystyle DI\) egyenesek \(\displaystyle HC'\)-n metszik egymást, azaz az \(\displaystyle I\) pont illeszkedik \(\displaystyle HC'\)-re, amiből az állítás következik.

Statisztika:

15 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Bodor Mátyás, Csonka Illés, Diaconescu Tashi, Gömze Norken, Holló Martin, Keresztély Zsófia, Kovács Benedek Noel, Romaniuc Albert-Iulian, Vigh 279 Zalán.
5 pontot kapott:	Forrai Boldizsár, Jármai Roland.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. áprilisi matematika feladatai