A B. 5394. feladat (2024. május)

B. 5394. Az $\displaystyle ABCD$ négyzet középpontja $\displaystyle O$, körülírt körének egy tetszőleges pontja $\displaystyle X$. Jelölje $\displaystyle T$ az $\displaystyle X$ merőleges vetületét $\displaystyle BC$-n. Legyen az $\displaystyle XB$ és $\displaystyle AC$ egyenesek metszéspontja $\displaystyle E$, az $\displaystyle XC$ és $\displaystyle BD$ egyeneseké pedig $\displaystyle F$. Mutassuk meg, hogy $\displaystyle EF$ merőleges $\displaystyle TO$-ra.

Javasolta: Vígh Viktor (Sándorfalva)

(4 pont)

A beküldési határidő 2024. június 10-én LEJÁRT.

Megoldás.

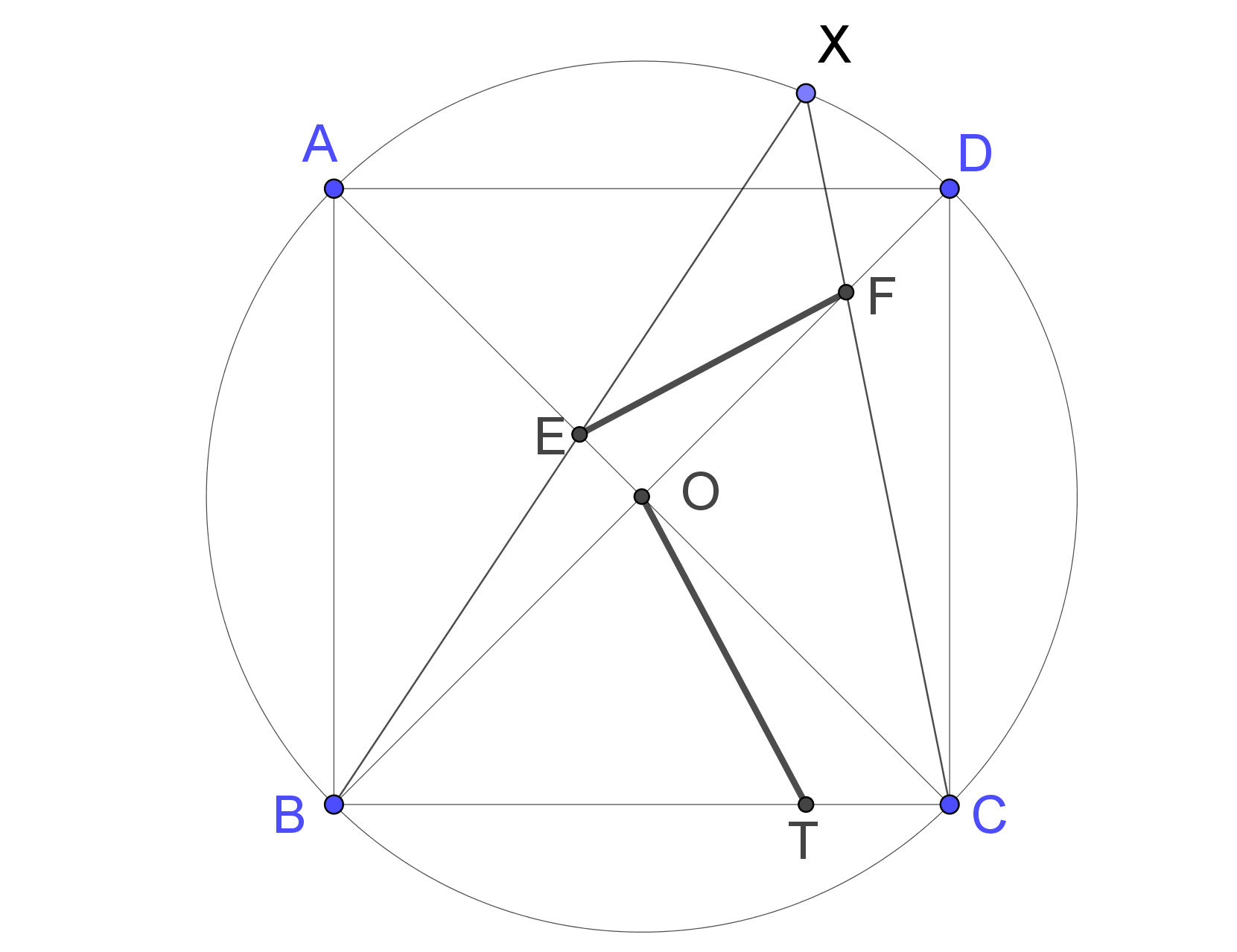
Legyen $\displaystyle O$ a koordináta-rendszer origója, jelölje továbbá az $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$, $\displaystyle X$, $\displaystyle E$, $\displaystyle F$, $\displaystyle T$ pontok koordinátáit rendre $\displaystyle (-1;1)$, $\displaystyle (-1;-1)$, $\displaystyle (1;-1)$, $\displaystyle (1;1)$, $\displaystyle (a;b)$, $\displaystyle (-e;e)$, $\displaystyle (f;f)$, $\displaystyle (a;-1)$. Ekkor

$\displaystyle \overrightarrow{EX} = (a+e;b-e), \overrightarrow{BE} = (-e+1;e+1).$

A két vektor párhuzamos, ezért $\displaystyle \frac{b-e}{a+e} = \frac{e+1}{-e+1}$, így $\displaystyle e=\frac{b-a}{a+b+2}$.

Hasonlóan, az

$\displaystyle \overrightarrow{FX} = (a-f;b-f), \overrightarrow{CF} = (f-1;f+1)$

vektorok párhuzamosak lévén $\displaystyle \frac{a-f}{b-f} = \frac{f-1}{f+1}$, amiből $\displaystyle f=\frac{a+b}{-a+b+2}$.

Legyen $\displaystyle N = (a+b+2)(-a+b+2)$; ekkor

$\displaystyle f+e = \frac{1}{N}((a+b)(a+b+2) + ((b-a)(-a+b+2)) = \frac{1}{N} (2a^2+2b^2+4b),$

és

$\displaystyle f-e = \frac{1}{N}((a+b)(a+b+2) - ((b-a)(-a+b+2)) = \frac{1}{N} (4ab+4a).$

Mindezek alapján

$\displaystyle \overrightarrow{EF} = (f+e;f-e) = \frac{1}{N}(2a^2+2b^2+4b;4ab+4a),$

így az $\displaystyle \overrightarrow{EF}$ és $\displaystyle \overrightarrow{OT}$ vektorok skaláris szorzata

$\displaystyle \frac{1}{N}((2a^2+2b^2+4b)a - (4ab+4a)) = \frac{2a(a^2+b^2-2)}{N}.$

Mivel $\displaystyle X$ a négyzet köré írt körön fekszik, $\displaystyle a^2+b^2 = OX^2 = OA^2 = 2$, vagyis a skaláris szorzat nulla, tehát a két vektor egymásra merőleges.

Statisztika:

40 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Aravin Peter, Bodor Mátyás, Bui Thuy-Trang Nikolett, Christ Miranda Anna, Csonka Illés, Csupor Albert Dezső, Dam Soham, Diaconescu Tashi, Erdélyi Kata, Farkas Ábel, Fehérvári Donát, Fekete Aron, Fórizs Emma, Forrai Boldizsár, Gömze Norken, Holló Martin, Jármai Roland, Keresztély Zsófia, Klement Tamás, Kovács Benedek Noel, Lakner Hanna, Op Den Kelder Ábel, Petrányi Lilla, Pletikoszity Martin, Prohászka Bulcsú, Puppi Barna, Romaniuc Albert-Iulian, Sági Mihály, Sha Jingyuan, Sütő Áron, Tamás Gellért, Török Eszter Júlia, Virág Lénárd Dániel, Virág Tóbiás.
3 pontot kapott:	Vigh 279 Zalán.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2024. májusi matematika feladatai