Problem B. 5396. (May 2024)

B. 5396. An equilateral pentagon in the three-dimensional space has four right angles. What can be its fifth angle?

(Proposed by Péter Dombi, Pécs)

(6 pont)

Deadline expired on June 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az ötszögünk \(\displaystyle ABCDE\), és tegyük fel, hogy a derékszögű csúcsok \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\). Válasszuk úgy a koordináta-rendszert, hogy \(\displaystyle A(0,0,0)\), \(\displaystyle B(1,0,0)\) és \(\displaystyle C(1,1,0)\). Mivel \(\displaystyle BCD\sphericalangle=90^\circ\), ezért \(\displaystyle D\) rajta van az \(\displaystyle y=1\) síkon, és így \(\displaystyle t\)-vel jelölve a \(\displaystyle \overrightarrow{CD}\) és \(\displaystyle x\)-tengely szögét kapjuk, hogy \(\displaystyle D(1+\cos t, 1, \sin t)\). Hasonlóan \(\displaystyle E(0,\cos u, \sin u)\), ahol \(\displaystyle u\) az \(\displaystyle \overrightarrow{AE}\) és \(\displaystyle y\)-tengely szöge. (\(\displaystyle D\) és \(\displaystyle E\) egy-egy egységnyi sugarú körön lehet.)

Kettő feltevést nem használtunk még ki, hogy \(\displaystyle D\)-nél is derékszög van, illetve hogy \(\displaystyle DE=1\). Előbbi ekvivalens azzal, hogy \(\displaystyle \overrightarrow{CD}\cdot \overrightarrow{DE}=0\). Mivel \(\displaystyle \overrightarrow{CD}=(\cos t , 0 , \sin t)\), és \(\displaystyle \overrightarrow{DE}=(-1-\cos t, \cos u -1, \sin u -\sin t)\), így a \(\displaystyle -\cos t -\cos^2 t + \sin t \sin u - \sin ^2 t=0\) egyenlethez jutunk, azaz

\(\displaystyle -\cos t + \sin t \sin u =1.\)

Másrészt \(\displaystyle DE=1\)-ből \(\displaystyle (1+\cos t)^2+(1-\cos u)^2+(\sin u -\sin t)^2=1\), amit kibontva és rendezve

\(\displaystyle 2\cos t - 2\cos u - 2 \sin u \sin t=-3.\)

Ezekből \(\displaystyle t\) és \(\displaystyle u\) értéke meghatározható. Az első egyenlet kétszeresét a másodikhoz adva \(\displaystyle \cos u =1/2\) adódik. Feltehetjük, hogy \(\displaystyle u=\pi/3\) (különben tükrözzük az ábrát az \(\displaystyle xy\)-síkra), s így \(\displaystyle E(0,1/2,\sqrt3/2)\).

Visszahelyettesítve \(\displaystyle u\) értékét az \(\displaystyle 1=\sqrt 3/2 \cdot \sin t- \cos t\) egyenletet kapjuk, amiből \(\displaystyle t_1=\pi\) és \(\displaystyle t_2\approx 1,71\). A \(\displaystyle t_1\)-hez a \(\displaystyle D(0,1,0)\) pont tartozik, ekkor az \(\displaystyle ADE\) háromszög szabályos, és a keresett ötödik szög \(\displaystyle 60^\circ\).

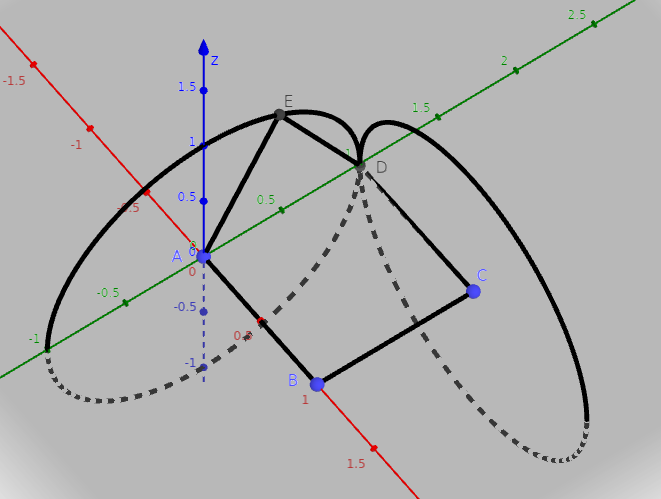
A \(\displaystyle t_2\)-höz a \(\displaystyle D(0,86;1;0,99)\) pont tartozik. Az \(\displaystyle \overrightarrow{EA}\) és \(\displaystyle \overrightarrow{ED}\) szögét leggyorsabban skalárszorzatból határozhatjuk meg, rutin számolás után

\(\displaystyle \cos \varphi=\frac {\overrightarrow{EA}\cdot \overrightarrow{ED}}{|\overrightarrow{EA}|\cdot |\overrightarrow{EA}|}\approx -0,36,\)

amiből a keresett szögre (körülbelül) \(\displaystyle 111^\circ\) adódik.

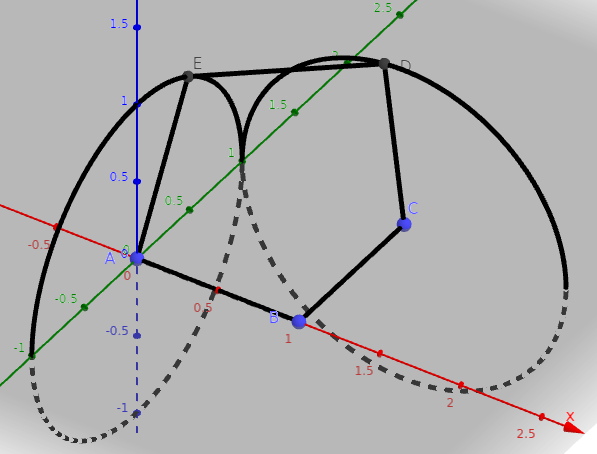
Két megoldást kaptunk, a keresett szög \(\displaystyle 60^\circ\) vagy (körülbelül) \(\displaystyle 111^\circ\) lehet.

Megjegyzések. 1. A számolás közelítések nélkül is elvégezhető trigonometrikus azonosságok felhasználásával, így a második esetre a \(\displaystyle \cos \varphi=-5/14\) pontos érték adódik.

2. Másképp is célt érhetünk: az \(\displaystyle ABE\) és \(\displaystyle CDE\) egyenlő szárú derékszögű háromszögek, emiatt a \(\displaystyle BCE\) háromszög oldalai \(\displaystyle 1\), \(\displaystyle \sqrt 2\), \(\displaystyle \sqrt 2\). Erre az adott háromszögre ,,ragasztjuk rá" az \(\displaystyle ABE\) és \(\displaystyle CDE\) egyenlő szárú, derékszögű háromszögeket úgy, hogy a \(\displaystyle B\), ill. \(\displaystyle C\) csúcsoknál is derékszöge legyen a kapott ötszögnek. Mindkét háromszög két-kétféleképpen ragaszható fel, de a kapott négy ötszögből kettő-kettő egybevágó. A számolás ezek alapján is elvégezhető, de ekkor is célszerű az ábrát valahogy elhelyezni egy koordinátarendszerben. Érdekes megjegyezni, hogy míg az első, \(\displaystyle 60^\circ\)-t adó konstrukció síkra szimmetrikus, addig a második, tompaszögű esetben a két egybevágó megoldás egymás tükörképe (szemléletesen van egy jobbos, és egy balos változat).

Statistics:

42 students sent a solution.
6 points:	Ali Richárd, Aravin Peter, Bencze Mátyás, Bodor Mátyás, Bui Thuy-Trang Nikolett, Erdélyi Kata, Hodossy Réka, Keresztély Zsófia, Kovács Barnabás, Kovács Benedek Noel, Pletikoszity Martin, Prohászka Bulcsú, Sárdinecz Dóra, Vigh 279 Zalán, Virág Tóbiás, Wágner Márton.
5 points:	Christ Miranda Anna, Dam Soham, Gyenes Károly, Holló Martin, Tulkán Dávid, Veres Dorottya.
4 points:	5 students.
3 points:	10 students.
2 points:	3 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, May 2024