A B. 5398. feladat (2024. szeptember)

B. 5398. Az $\displaystyle ABCD$ trapézban $\displaystyle AB \parallel CD$ és $\displaystyle ADC \sphericalangle - CBA \sphericalangle = 90^{\circ}$. Igazoljuk, hogy a szárak négyzetének összege egyenlő az alapok különbségének négyzetével.

Javasolta: Oláh Miklós, Szilágykraszna

(3 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás. A trapéz oldalainak hosszúsága legyen $\displaystyle AB=a$, $\displaystyle BC=b$, $\displaystyle CD=c$, $\displaystyle DA=d$. A $\displaystyle D$ ponton átmenő, $\displaystyle BC$-vel párhuzamos egyenesnek az $\displaystyle AB$ alappal közös pontját jelölje $\displaystyle E$.

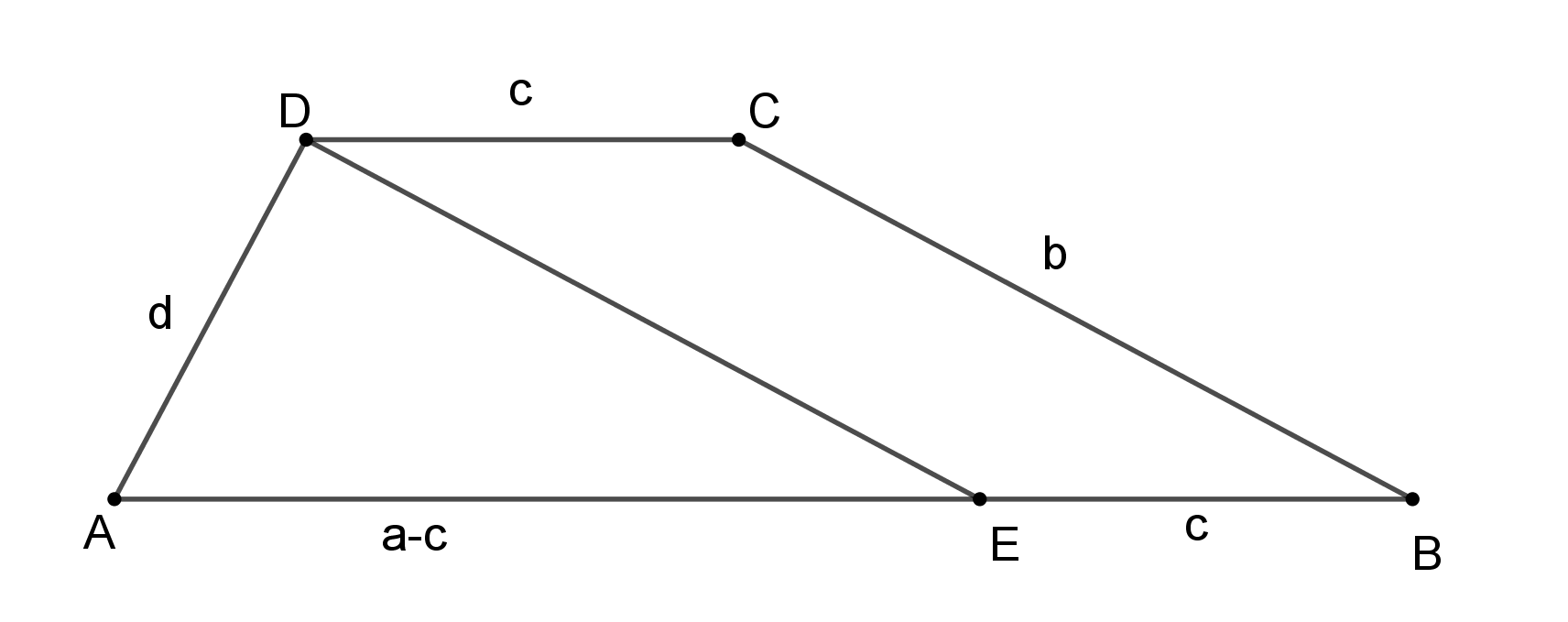
Az $\displaystyle EBCD$ négyszög szemköztes oldalai párhuzamosak lévén $\displaystyle EBCD$ paralelogramma, ezért $\displaystyle EB=c$, így $\displaystyle AE=a-c$, továbbá $\displaystyle ED=b$ és $\displaystyle EDC\sphericalangle=CBA\sphericalangle$. Ezért $\displaystyle ADE\sphericalangle = ADC\sphericalangle - EDC\sphericalangle = ADC\sphericalangle - CBA\sphericalangle = 90^{\circ}$. Az $\displaystyle AD=d$, $\displaystyle ED=b$ befogójú, $\displaystyle AE=a-c$ átfogójú derékszögű háromszögben Pitagorasz tétele szerint $\displaystyle d^2+b^2=(a-c)^2$.

Statisztika:

176 dolgozat érkezett.
3 pontot kapott:	115 versenyző.
2 pontot kapott:	24 versenyző.
1 pontot kapott:	16 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	10 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai