A B. 5402. feladat (2024. szeptember)

B. 5402. Egy háromszög oldalainak hosszúsága $\displaystyle a$, $\displaystyle b$, $\displaystyle c$. Tegyük fel, hogy fennáll

$\displaystyle a^2+b^2+c^2 = a^2b^2c^2.$

Bizonyítandó, hogy a háromszög területe legfeljebb $\displaystyle \frac34$, és egyenlőség csak az egyenlő oldalú háromszög esetében lehetséges.

Javasolta: Hujter Mihály, Budapest

(5 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás.

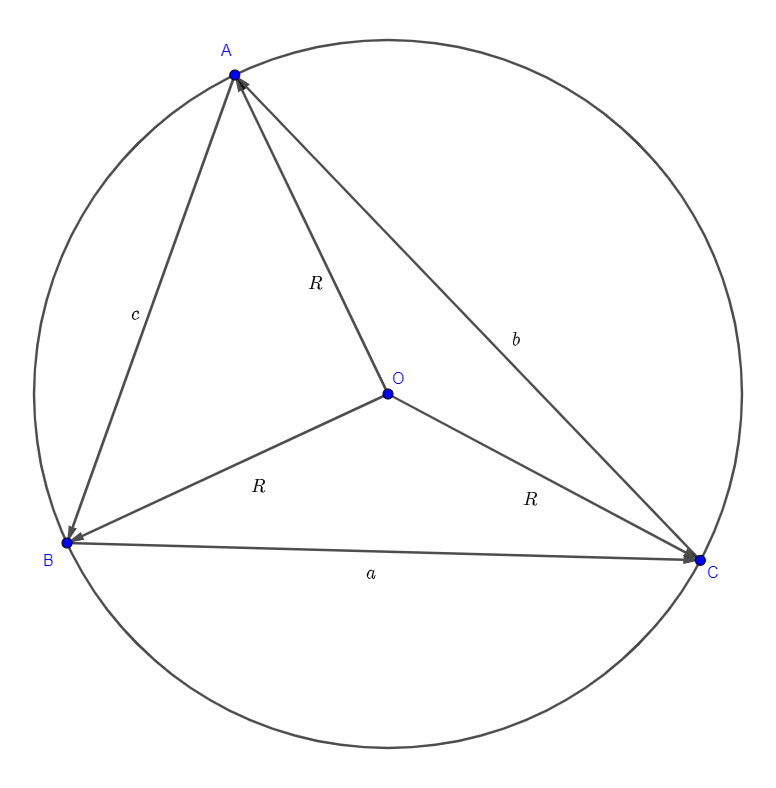
Legyenek a háromszög a csúcsai $\displaystyle A$, $\displaystyle B$ és $\displaystyle C$, a körülírt kör középpontja $\displaystyle O$, sugara $\displaystyle R$. Emeljük négyzetre az $\displaystyle \overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{AB}$ egyenlőséget. Mivel $\displaystyle |\overrightarrow{AB}|=c$ és $\displaystyle |\overrightarrow{OA}|=|\overrightarrow{OB}|=R$, így kapjuk, hogy $\displaystyle 2R^2-2\cdot\overrightarrow{OA}\cdot \overrightarrow{OB}=c^2$; átrendezve $\displaystyle 2\cdot\overrightarrow{OA}\cdot\overrightarrow{OB}=2R^2-c^2$. Hasonlóan láthatjuk, hogy $\displaystyle 2\cdot\overrightarrow{OA}\cdot\overrightarrow{OC}=2R^2-b^2$ és $\displaystyle 2\cdot\overrightarrow{OB}\cdot\overrightarrow{OC}=2R^2-a^2$.

Ezek alapján

$\displaystyle 0\le (\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})^2=\overrightarrow{OA}^2+\overrightarrow{OB}^2+\overrightarrow{OC}^2+2\cdot\overrightarrow{OA}\cdot\overrightarrow{OB}+2\cdot\overrightarrow{OA}\cdot\overrightarrow{OC}+2\cdot\overrightarrow{OB}\cdot\overrightarrow{OC}=3R^2+2R^2-c^2+2R^2-b^2+2R^2-a^2;$

vagy rendezve

$\displaystyle a^2+b^2+c^2\le 9R^2.$

Jól ismert, hogy a háromszög területe $\displaystyle T=abc/4R$ képlettel számítható. Ebből kiindulva, felhasználva a feladat feltételét és az előbb igazolt egyenlőtlenséget kapjuk, hogy

$\displaystyle 16T^2=\frac{a^2b^2c^2}{R^2}=\frac{a^2+b^2+c^2}{R^2}\le 9.$

Ebből gyököt vonva kapjuk a feladat állítását.

A gondolatmenetben egyetlen helyen alkalmaztunk becslést, ezért egyenlőség pontosan akkor áll, ha $\displaystyle 0= (\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})^2$, azaz $\displaystyle \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ a nullvektor. Mivel $\displaystyle |\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|=R$, ez azt jelenti, hogy az $\displaystyle \overrightarrow{OA}+\overrightarrow{OB}$ vektor is $\displaystyle R$ hosszúságú. Ebből a vektorösszeadás definíciója miatt következik, hogy az $\displaystyle \overrightarrow{OA}$ és $\displaystyle \overrightarrow{OB}$ vektorok szöge $\displaystyle 120^\circ$. Hasonlóan érvelhetünk $\displaystyle \overrightarrow{OA}$ és $\displaystyle \overrightarrow{OC}$, valamint $\displaystyle \overrightarrow{OB}$ és $\displaystyle \overrightarrow{OC}$ esetén. Ebből következik, hogy az $\displaystyle ABC$ háromszög szabályos kell legyen, amikor valóban egyenlőség teljesül.

Megjegyzések.

1. Jól ismert, hogy $\displaystyle \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM},$ ahol $\displaystyle M$ a magasságpont. Egyenlőség tehát pontosan $\displaystyle O=M$ esetben áll.

2. A szinusz-tétel szerint

$\displaystyle 4\sin^2 \alpha+4\sin^2 \beta+4\sin^2 \gamma=\frac{a^2+b^2+c^2}{R^2}.$

Ebből következik, hogy a feladat állítása ekvivalens (az egyébként közismert)

$\displaystyle \sin^2 \alpha+\sin^2 \beta+\sin^2 \gamma \le \frac 94$

egyenlőtlenséggel.

3. Trigonometrikus azonosságok alkalmazásával belátható, hogy $\displaystyle \sin^2 \alpha+\sin^2 \beta+\sin^2 \gamma=2+2\cos \alpha\cos \beta\cos \gamma$. Azaz a feladat ekvivalens a

$\displaystyle \cos \alpha\cos \beta \cos \gamma\le \frac 18$

egyenlőtlenséggel is. Ez az egyenlőtlenség pedig következik a nevezetes koszinusz-egyenlőtlenségből:

$\displaystyle \cos \alpha+\cos \beta+\cos \gamma\le \frac 32.$

Lásd még Reiman István, Dobos Sándor: Nemzetközi Matematikai Diákolimpiák könyvben az 1964/2. feladatot és megoldását, valamint a könyv végén a [12] kiegészítést.

Statisztika:

79 dolgozat érkezett.
5 pontot kapott:	Ali Richárd, Aravin Peter, Bodor Ádám, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Görömbey Tamás, Gyenes Károly, Holló Martin, Kerekes András, Kovács Benedek Noel, Kővágó Edit Gréta, Ma Martin, Molnár István Ádám, Pázmándi József Áron, Prohászka Bulcsú, Sajter Klaus, Sánta Gergely Péter, Sha Jingyuan, Sütő Áron, Tóth 207 Bence, Virág Lénárd Dániel, Virág Tóbiás, Wágner Márton.
4 pontot kapott:	Bencze Mátyás, Dancs Bálint, Forrai Boldizsár, Klement Tamás, Máté Marcell, Pletikoszity Martin, Szabó 721 Sámuel, Veres Dorottya, Vigh 279 Zalán, Vödrös Dániel László, Zhai Yu Fan.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	21 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai