A B. 5403. feladat (2024. szeptember)

B. 5403. Tegyük fel, hogy egy egyszerű, összefüggő \(\displaystyle k\)-reguláris (\(\displaystyle k \ge 2\)) \(\displaystyle G\) gráf éleit ki lehet színezni \(\displaystyle k\) színnel úgy, hogy minden csúcsban csupa különböző színű él találkozzon. Bizonyítsuk be, hogy \(\displaystyle G\) bármelyik élét törölve a kapott gráf is összefüggő.

Javasolta: Hujter Bálint, Budapest

(5 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás. Színezzük ki a gráf éleit \(\displaystyle k\) színnel úgy, hogy minden csúcsban csupa különböző színű él találkozzon. Ilyenkor, ha egyet kiválasztunk a \(\displaystyle k\) szín közül, és csak az ilyen színű éleket tekintjük, akkor észrevehetjük, hogy minden csúcsba pont egy ilyen színű él fut be, ezek az élek tehát teljes párosítást alkotnak. (Mellékes következmény, hogy a gráf csúcsszáma biztosan páros).

Indirekt tegyük fel, hogy az \(\displaystyle e\) él törlésével szétesik a gráf, azaz a keletkező \(\displaystyle G'\) gráf már nem összefüggő.

\(\displaystyle G'\) tehát nem összefüggő, de kettőnél több komponense sem lehet, hiszen az \(\displaystyle e\) él csak kettőt tud összekötni a komponensek közül (és \(\displaystyle e\) visszatevésével összefüggővé kellene válnia a gráfnak).

Legyen az \(\displaystyle e\) él színe piros, egy másik szín a \(\displaystyle k\) közül pedig kék. A fentiek szerint a törlés előtt a piros élek teljes párosítást alkottak, tehát \(\displaystyle G'\)-ben is igaz, hogy a piros élek az \(\displaystyle e\) él két végén kívül a többi csúcsot bepárosítják. A pároknak egyazon komponensben kell lenniük, míg az \(\displaystyle e\) véginek különböző komponensben. Tehát a két komponens külön-külön páratlan sok csúccsal rendelkezik.

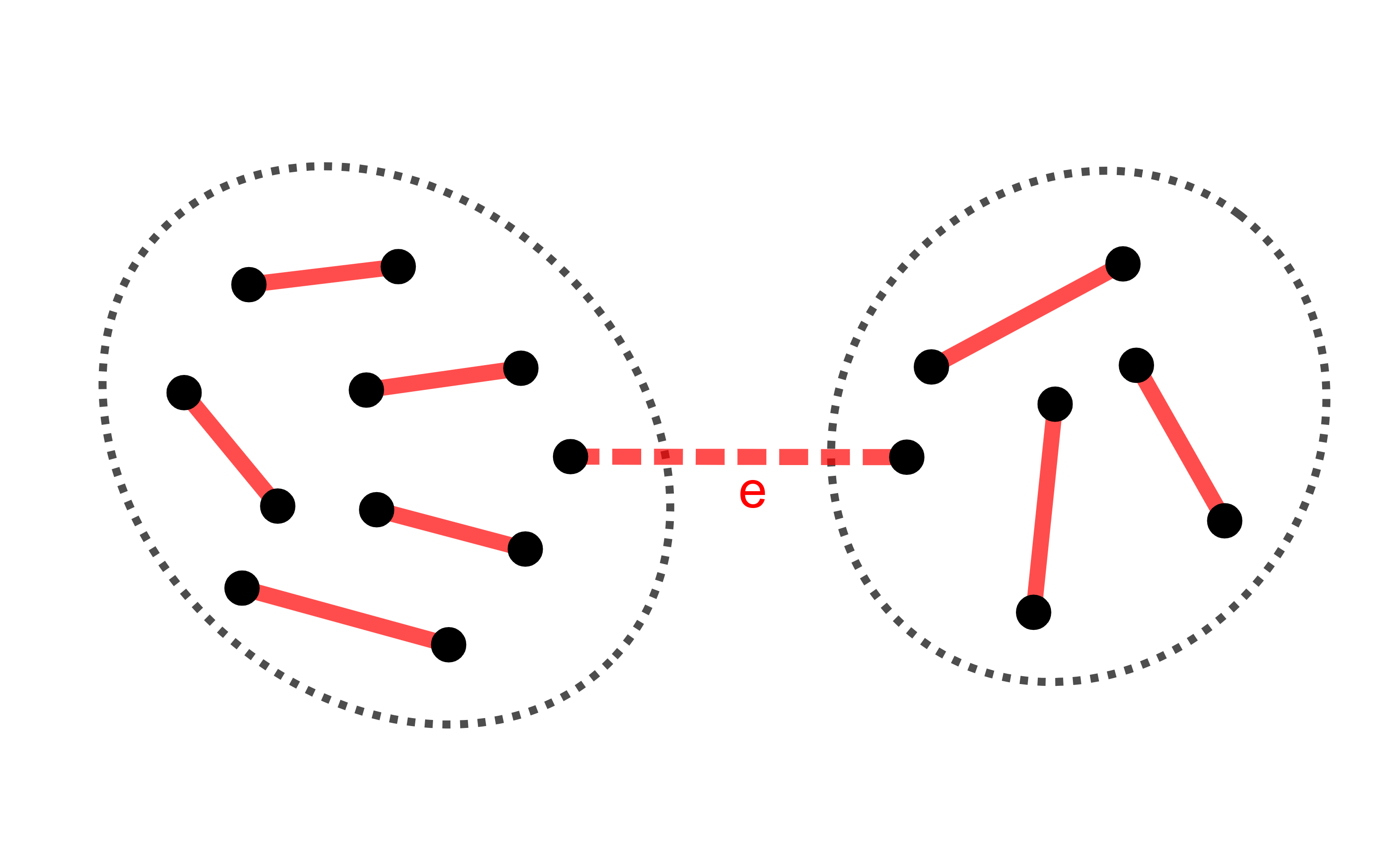
A kék élek ugyanakkor \(\displaystyle G'\)-ben is teljes párosítást alkotnak. Mivel a kék szín szerinti pároknak is egyazon komponensben kell lenniük, ezért minden komponens páros elemszámú kell legyen. Ellentmondás.

Tehát bármelyik élét is töröljük, \(\displaystyle G\) összefüggő marad.

(Ezt úgy is szokás mondani, hogy \(\displaystyle G\) kétszeresen él-összefüggő. Nem tévesztendő össze a kétszeresen összefüggő – avagy kétszeresen csúcs-összefüggő – gráfok fogalmával, amelyek tetszőleges csúcs törlése után is összefüggők maradnak. Minden kétszeresen összefüggő gráf kétszeresen él-összefüggő is, de fordítva már nem igaz.)

Statisztika:

72 dolgozat érkezett.
5 pontot kapott:	52 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	7 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai