Problem B. 5404. (September 2024)

B. 5404. The altitudes of the acute triangle $\displaystyle ABC$ are $\displaystyle AT_A$, $\displaystyle BT_B$ and $\displaystyle CT_C$. The midpoints of the sides $\displaystyle BC$, $\displaystyle CA$ and $\displaystyle AB$ are $\displaystyle F_A$, $\displaystyle F_B$ and $\displaystyle F_C$, respectively. Let $\displaystyle r$ denote the radius of the inscribed circle and let $\displaystyle P_A$ denote the point on altitude $\displaystyle AT_A$ satisfying $\displaystyle AP_A = r$. Points $\displaystyle P_B$ and $\displaystyle P_C$ are defined similarly. Prove that line segments $\displaystyle F_AP_A$, $\displaystyle F_BP_B$ and $\displaystyle F_CP_C$ are concurrent.

Proposed by Géza Kiss, Csömör

(6 pont)

Deadline expired on October 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Azt fogjuk belátni, hogy a feladatban szereplő szakaszok a háromszög beírt körének középpontjában metszik egymást.

Hegyesszögű egyenlőszárú (vagy egyenlő oldalú) háromszög esetén az alaphoz tartozó megfelelő szakasz mindenképpen átmegy a beírt kör középpontján, így elegendő olyan esetet tárgyalnunk, amikor az oldal felezőpontja és a magasságvonal feladatban definiált pontja nem a belső szögfelezőre esnek. Legyenek ezek az $\displaystyle F_A$ és $\displaystyle P_A$ pontok.

Jelöljük a felsoroltakon kívül a beírt kör középpontját $\displaystyle I$-vel, a háromszög $\displaystyle A$-nál fekvő szögét $\displaystyle \alpha$-val, a beírt kör érintési pontja az $\displaystyle AC$ oldalon legyen $\displaystyle E$, továbbá messe az $\displaystyle F_AI$ félegyenes az $\displaystyle AT_A$ magasságvonalat az $\displaystyle X$ pontban. Be fogjuk látni, hogy $\displaystyle X\equiv P_A$.

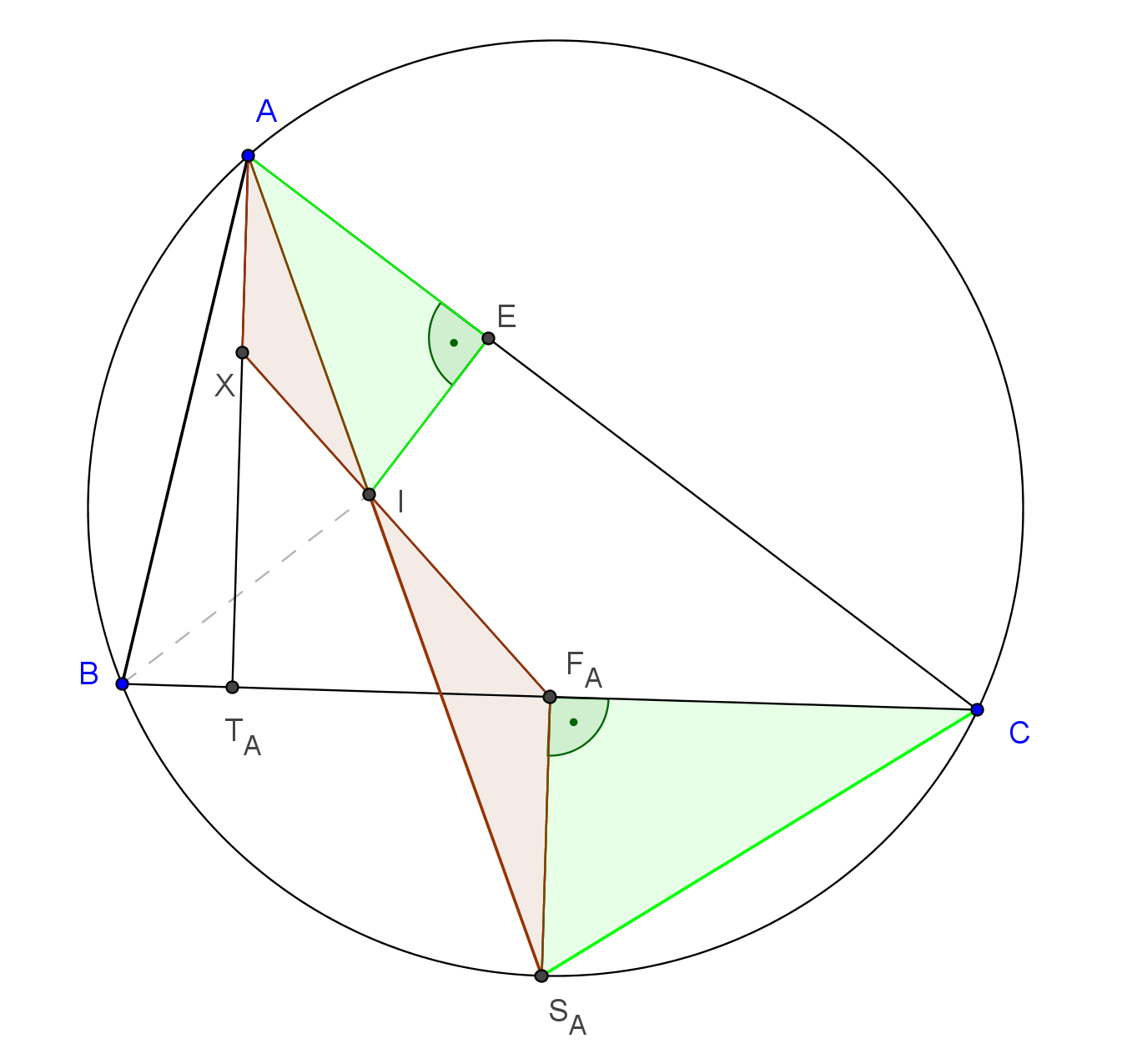
Ismertnek tételezzük fel egyrészt, hogy az $\displaystyle A$-hoz tartozó belső szögfelező és a $\displaystyle BC$ oldal felezőmerőlegese a körülírt körön, mégpedig a $\displaystyle BC$ körív $\displaystyle S_A$ felezőpontjában metszik egymást. Másrészt szintén sokszor előforduló tény, hogy ez az $\displaystyle S_A$ pont egyenlő távolságra van a beírt kör középpontjától és a $\displaystyle B, ~C$ csúcsoktól. (Ld. pl. a B5291. feladatban szereplő lemma megoldását: https://www.komal.hu/feladat?a=feladat&f=B5291&l=hu).

Az $\displaystyle AXI\triangle \sim S_AF_AI\triangle$, mert az $\displaystyle I$-nél lévő szögeik csúcsszögek, míg $\displaystyle XAI\sphericalangle$ és $\displaystyle F_AS_AI$ váltószögek. Az oldalak arányára teljesül, hogy

$\displaystyle \frac{AX}{AI}=\frac{F_AS_A}{S_AI}.\tag{1}$

Szintén hasonlóak az $\displaystyle S_AF_AC$ és $\displaystyle IEA$ háromszögek, mert az $\displaystyle E$-nél és $\displaystyle F_A$-nál derékszögek vannak, továbbá az $\displaystyle EAI\sphericalangle$ és $\displaystyle F_ACS_A\sphericalangle$ szögek a $\displaystyle BS_A$, $\displaystyle CS_A$ egyenlő körívekhez tartozó kerületi szögek, tehát szintén egyenlők. Az oldalak arányának egyenlőségéből itt:

$\displaystyle \frac{F_AS_A}{S_AC}=\frac{EI}{AI}=\frac{r}{AI}.\tag{2}$

(1) és (2) összevetéséből, felhasználva, hogy $\displaystyle S_AI=S_AC$ kapjuk, hogy

$\displaystyle \frac{AX}{AI}=\frac{F_AS_A}{S_AI}=\frac{F_AS_A}{S_AC}=\frac{EI}{AI}=\frac{r}{AI}.$

Ezek szerint $\displaystyle AX=r$, tehát a $\displaystyle P_A$ pont egybeesik az $\displaystyle X$ ponttal.

Ezzel megmutattuk, hogy az $\displaystyle F_AP_A$ szakasz valóban átmegy a beírt kör középpontján. Az $\displaystyle F_BP_B$ és $\displaystyle F_CP_C$ szakaszokra ugyanígy végezhető el a bizonyítás; a három szakasz a beírt kör középpontjában metszi egymást.

Statistics:

40 students sent a solution.
6 points:	Ali Richárd, Aravin Peter, Bodor Ádám, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Erdélyi Kata, Fekete Aron, Forrai Boldizsár, Gyenes Károly, Hodossy Réka, Holló Martin, Horák Zsófia, Kovács Benedek Noel, Pázmándi József Áron, Prohászka Bulcsú, Sárdinecz Dóra, Sha Jingyuan, Szabó 721 Sámuel, Vámosi Bendegúz Péter, Vigh 279 Zalán, Virág Tóbiás, Wágner Márton, Zhai Yu Fan.
5 points:	Bencze Mátyás, Bodor Noémi, Kővágó Edit Gréta, Li Mingdao, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Virág Lénárd Dániel, Vödrös Dániel László.
4 points:	1 student.
2 points:	3 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, September 2024