 |
A B. 5410. feladat (2024. október) |
B. 5410. Egy derékszögű háromszög csúcsai köré úgy írunk köröket, hogy egymást páronként kívülről érintik. Határozzuk meg annak a körnek a középpontját és sugarát, amelyet mindhárom kör belülről érint.
Javasolta: Németh László (Fonyód)
(5 pont)
A beküldési határidő 2024. november 11-én LEJÁRT.
Megoldás. Betűzzük meg a háromszög csúcsait és oldalait a szokásos módon, vagyis legyen a derékszögű csúcs \(\displaystyle C\), a beírt kör középpontja \(\displaystyle I\), a \(\displaystyle B\) és \(\displaystyle C\) körül írt körök érintsék egymást kívülről a \(\displaystyle BC\) oldalon az \(\displaystyle E\) pontban, az \(\displaystyle A\) és \(\displaystyle C\) körül írt körök pedig az \(\displaystyle AC\) oldalon az \(\displaystyle F\) pontban. Legyenek az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) körül írt egymást érintő körök sugarai rendre \(\displaystyle x, y\) és \(\displaystyle z\). A sugarakat a következő egyenletrendszerből határozhatjuk meg:
$$\begin{align*} x+y=c,\\ y+z=a,\\ z+x=b. \end{align*}$$A három egyenletet összeadva:
\(\displaystyle 2x+2y+2z=a+b+c=2s, \quad \text{azaz} \quad x+y+z=s.\)
Innen már azonnal kapjuk, hogy
\(\displaystyle x=s-(y+z)=s-a, \quad y=s-b, \quad z=s-c. \)
Tekintsük azt a \(\displaystyle k\) kört, amelynek sugara \(\displaystyle s\), középpontja pedig a derékszögű \(\displaystyle C\) csúcsnak az átfogó felezőpontjára vonatkozó tükörképe, amit jelöljön \(\displaystyle K\). Nyilvánvalóan \(\displaystyle ACBK\) egy téglalap. Ekkor az \(\displaystyle AK\) távolságra \(\displaystyle AK=a=s-(s-a)\), így \(\displaystyle k\) belülről érinti az \(\displaystyle A\) középpontú \(\displaystyle s-a\) sugarú kört. Ugyanígy \(\displaystyle KB\) távolságra \(\displaystyle KB=b=s-(s-b)\), s \(\displaystyle CK\) távolságra \(\displaystyle CK=c=s-(s-c)\), azaz \(\displaystyle k\) belülről érinti a \(\displaystyle B\) és \(\displaystyle C\) körüli köröket is.
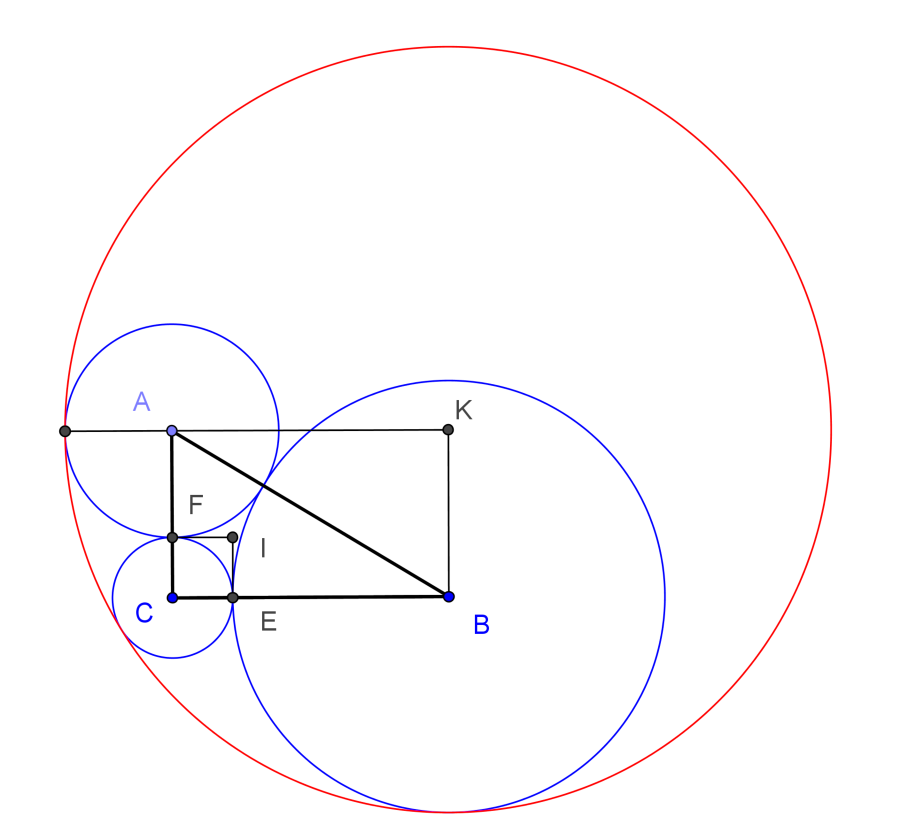
Azt állítjuk, hogy \(\displaystyle k\) az egyetlen megoldás. Ennek bizonyításához invertáljuk a három csúcs körüli, egymást érintő kört egy olyan körre, amelynek középpontja a \(\displaystyle BC\) oldal első részben tárgyalt \(\displaystyle E\) pontja (lila színnel) . Tudjuk, hogy a \(\displaystyle B\) és \(\displaystyle C\) körüli körök érintik egymást ebben a pontban, tehát inverz képük két párhuzamos egyenes lesz. Ezeket a köröket és egyeneseket az ábrán zöld színnel jelöltük.

A párhuzamosokat érinti az \(\displaystyle A\) körüli kör inverze. Ez szintén kör. (Ezt a két kört barna színnel jelöltük.) A mindhárom kört érintő kör keresése helyett az inverzió utáni helyzetben olyan kör(öke)t keresünk, amelyek a két párhuzamos egyenest és közöttük elhelyezkedő kört érintik. Ilyen kör pontosan kettő van, amelyek közül egyik éppen annak a körnek az inverze, amelyet mindhárom adott kör belülről érint (piros szín), a másik pedig annak a körnek az inverze, amelyet kívülről érintenek (kék szín).
Tehát valóban csak egy megfelelő kör van, aminek középpontja \(\displaystyle K\), sugara pedig a háromszög félkerülete.
Statisztika:
A B. 5410. feladat értékelése még nem fejeződött be.
A KöMaL 2024. októberi matematika feladatai
