A B. 5413. feladat (2024. október)

B. 5413. Legyen az $\displaystyle ABC$ nem szabályos háromszög magasságpontja $\displaystyle M$, súlypontja $\displaystyle S$, beírt körének középpontja $\displaystyle I$. Mutassuk meg, hogy $\displaystyle MIS\sphericalangle>90^\circ$.

Javasolta: Vígh Viktor (Sándorfalva)

(6 pont)

A beküldési határidő 2024. november 11-én LEJÁRT.

Megoldás. Használjuk a szokásos jelöléseket, a körülírt kör középpontja legyen $\displaystyle O$. A koszinusztétel miatt elegendő lenne megmutatni, hogy $\displaystyle MS^2-IS^2-IM^2>0.$

Ehhez először is elevenítsük fel, hogy az $\displaystyle M$, $\displaystyle S$ és $\displaystyle O$ pontok a háromszög Euler-egyenesén helyezkednek el, $\displaystyle S$ az $\displaystyle MO$ szakasz $\displaystyle O$-hoz közelebbi harmadolópontja. Írjuk fel az $\displaystyle MOI$ háromszögben a Stewart-tételt az $\displaystyle IS$ szakaszra:

$\displaystyle IM^2\cdot SO+IO^2\cdot MS=MO\cdot IS^2+MO\cdot MS\cdot SO.$

Felhasználva, hogy $\displaystyle S$ harmadol, osszuk mindkét oldalt $\displaystyle SO$-val, s így nyerjük, hogy

$\displaystyle IM^2+2IO^2=3IS^2+MO\cdot MS=3IS^2+\frac 32 MS^2.$

Ebből rendezéssel adódik, hogy

$\displaystyle IS^2=\frac 23 IO^2+ \frac 13 IM^2-\frac 12 MS^2.$

Ezt behelyettesítve $\displaystyle IS^2$ helyére:

$\displaystyle MS^2-IS^2-IM^2=MS^2-\frac 23 IO^2- \frac 13 IM^2+\frac 12 MS^2-IM^2=\frac 32 MS^2-\frac 23 IO^2-\frac 43 IM^2=\frac 23\left (MO^2- IO^2-2 IM^2 \right ).$

A továbbiakban a zárójelben lévő kifejezésről igazoljuk, hogy pozitív. Először is az Euler-tétel szerint $\displaystyle IO^2=R^2-2Rr$, ahol $\displaystyle R$ és $\displaystyle r$ rendre a körülírható- és a beírható körök sugarai.

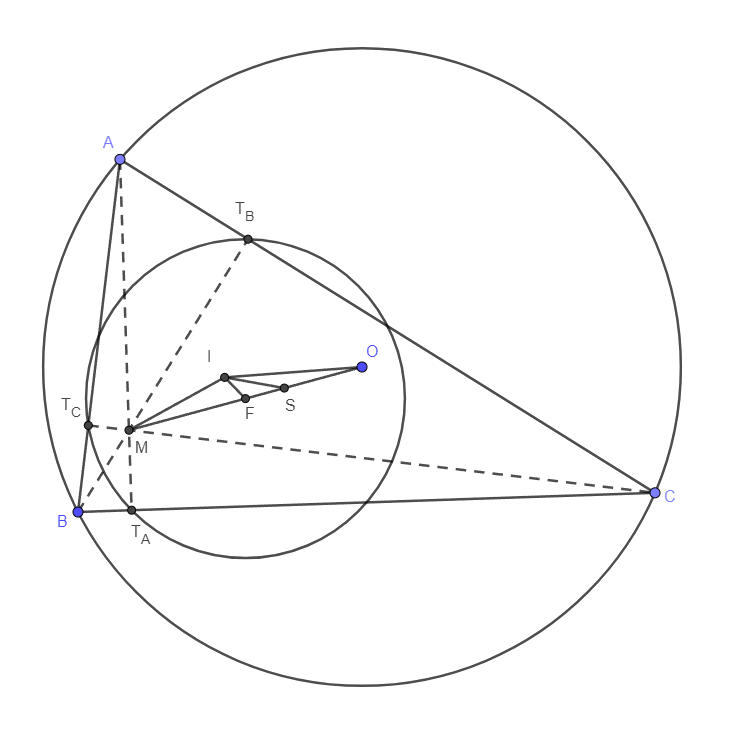
Tekintsük az $\displaystyle ABC$ háromszög Feuerbach-körét, ennek sugara $\displaystyle R/2$, középpontja pedig az $\displaystyle MO$ szakasz $\displaystyle F$ felezőpontja. A Feuerbach-tétel szerint ezen kört belülről érinti a beírt kör, ezért $\displaystyle IF=R/2-r$.

Írjuk fel a (paralelogramma-tételből vagy a fentebb idézett Stewart-tételből következő) összefüggést az $\displaystyle IMO$ háromszög $\displaystyle IF$ súlyvonalára:

$\displaystyle 2IM^2+2IO^2 = MO^2 + 4IF^2.$

Ebből

$\displaystyle MO^2-IO^2-2IM^2=IO^2-4IF^2=R^2-2Rr-4\left (\frac R2-r\right )^2=2Rr-4r^2=2r(R-2r).$

A sugáregyenlőtlenség szerint $\displaystyle R\ge 2r$ és egyenlőség csak szabályos háromszög esetén áll, így esetünkben $\displaystyle MO^2-IO^2-2IM^2>0$, amivel a feladat állítását beláttuk.

Megjegyzés. Legyenek $\displaystyle T_A$, $\displaystyle T_B$ és $\displaystyle T_C$ a megfelelő magasságok talppontjai. Jól ismert tény, hogy a $\displaystyle T_AT_BT_C$ talpponti háromszög beírt körének középpontja éppen $\displaystyle M$, ezen beírt kör sugarát jelölje $\displaystyle \varrho$. A talpponti háromszög körülírt köre pedig éppen az $\displaystyle ABC$ háromszög Feuerbach-köre. Így viszont ismét alkalmazhatjuk az Euler-tételt, ezúttal a talpponti háromszögre, és így kapjuk, hogy

$\displaystyle OM^2=4MF^2=4\left [ \left (\frac R2\right )^2-2\cdot \frac R2 \cdot \varrho \right]=R^2-4R\varrho.$

A megoldásban is használt $\displaystyle 4IF^2=2IO^2+2IM^2-OM^2$ összefüggésből pedig $\displaystyle IM^2=2r^2-2R\varrho$ adódik, így végül $\displaystyle MO^2$, $\displaystyle IO^2$ és $\displaystyle IM^2$ mindegyikére elegáns formula adható $\displaystyle R$, $\displaystyle r$ és $\displaystyle \varrho$ segítségével.

Statisztika:

28 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Bencze Mátyás, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Holló Martin, Kovács Benedek Noel, Prohászka Bulcsú, Sha Jingyuan, Virág Lénárd Dániel.
5 pontot kapott:	Aravin Peter, Molnár Lili, Varga 511 Vivien, Zhai Yu Fan.
4 pontot kapott:	4 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2024. októberi matematika feladatai